Az origamis ördöglakatokkal foglalkozó cikkben beszéltünk különböző testek hálójáról. Vagyis olyan egymáshoz kapcsolódó sokszögekről, amikből hajtogatással előállítható a test. Egy kocka felszíne 6 négyzetből áll, így a kocka (legegyszerűbb) hálói 6 négyzetből álló hexominók. Éppen az origamis poszt írása közben jutott eszembe, hogy érdemes lenne megvizsgálni azt az összerakós játékot, aminek az elemei a kockahálók. Az összes hexominó annyira bonyolult játékot eredményez, hogy emberi aggyal szinte lehetetlen megoldani feladványait. Így jó kompromisszumnak tűnt a kockahálók vizsgálata, hisz azokból csak 11-féle létezik:

A jobb láthatóság érdekében következzenek ugyanezek rajzban is:
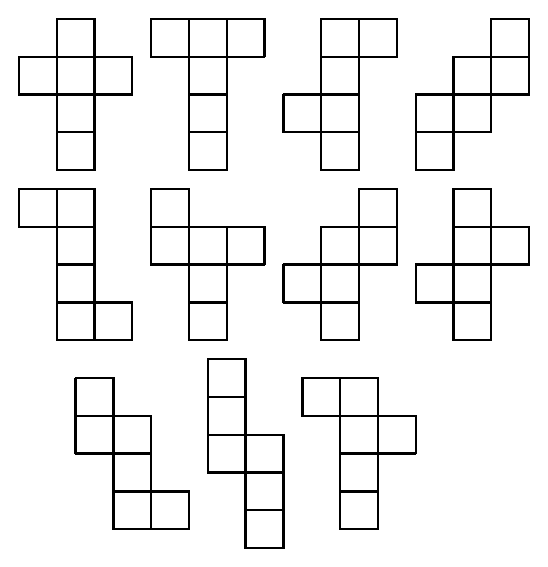
A 11 hexominó elem összesen 66 négyzetből áll, adódik első feladványnak a 6×11-es téglalap:
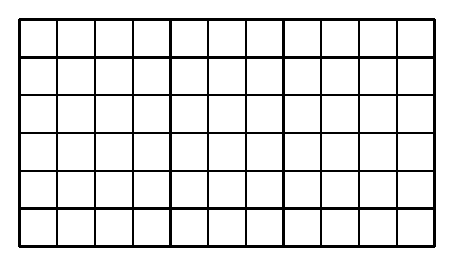
Sajnos, ez nem rakható ki a kockahálókból. Sebaj, vizsgáljunk néhány szintén 66 mezőből álló "lépcsőt":
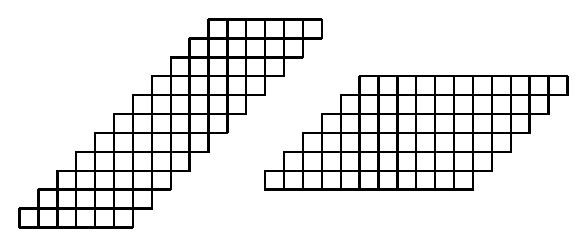
Hát, ezeknek sincs megoldása.
Ekkor már kezdett bosszantani a dolog. Gondoltam, 60 négyzet talán több sikerrel kecsegtet, ráadásul rengeteg feladvány létezik, ami pont ennyi mezőt tartalmaz, hisz a pentominók is ennyiből állnak. Sőt, egy elemet így el is lehet hagyni, ezzel is növelve a lehetőségek számát.
Kezdjük a téglalapokkal! Ezt már nagyobb meló volt kipróbálgatni, de ismét jártam sikerrel. Akárhogy választunk ki 10 elemet a 11 háló közül, sehogy nem lehet kirakni egyik 60 mezőből álló téglalapot sem, se a 3×20-ast, se a 4×15-öst, se az 5×12-est, se a 6×10-est.
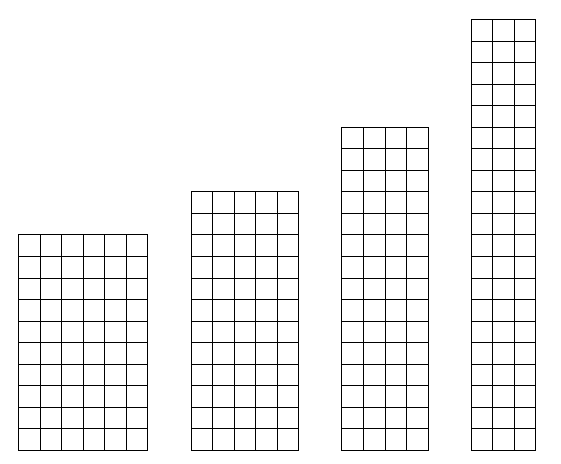
Akkor nézzünk pár szép, szimmetrikus sakktáblát! Van néhány:
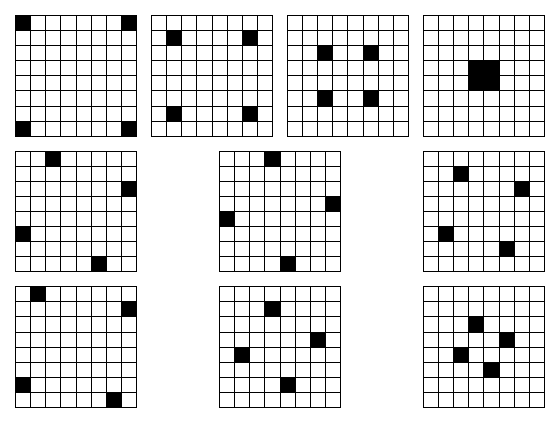
De ezeknek sem létezik megoldása.
No, egyelőre itt tartok. Nem találtam még "épkézláb" feladványt, amit a kockahálókkal lehetne megoldani.
Hátha az olvasónak sikerül valami szép alakzatot kirakni ezekből az utálatos elemekből!




