A blog egyik első bejegyzésében már foglalkoztunk facsomókkal. Futólag már ott is említettem a ketrecbe zárt csomókat, de annyira ötletesnek tartom, hogy szerintem megért egy külön cikket is. A ketrecbe zárt kockáknál már láttuk, hogy egy nem túl bonyolult játékból hogyan lesz igazán komoly fejtörő egy ketrec segítségével.
A három elemű facsomó az egyik legegyszerűbb az összekapcsolódó játékok közül. Vajon ezt is érdekesebbé, bonyolultabbá teszi egy kalitka?
A cél tehát az, hogy a facsomót juttassuk be egy ketrec belsejébe:

A ketrec akkora, hogy a csomót csak szétszedve lehet bejuttatni, vagyis a ketrec belsejében kell összerakni. A következő képen a méretek szemléltetésére egy összerakott csomó látható a ketrec belsejében is:

Látható, hogy pontosan olyan széles négyzetek a ketrec oldalai, mint a csomó rövidebb oldala. Így a csomó elemi két irányban mozoghatnak, a harmadik irányt gátolja a ketrec. Aki próbálkozott az eredeti csomó összerakásával, az bizonyára fel tudja idézni, hogy ott bizony volt elem, amit olyan irányban kellett mozgatni, amit ez a ketrec nem enged! Így, sajnos, az eredeti csomó nem rakható be a ketrecbe.
Szerencsére Tom Jolly nem elégedett meg a nemleges válasszal, hanem megpróbált olyan elemeket keresni, amik mégis valahogy beilleszthetők. Nem ragaszkodott a kívülről tömörnek tűnő csomóhoz, hanem csak azt tűzte ki célul, hogy a ketrec minden oldalán középen legyen egy teljes hosszúságú oldal. Ilyen feltételekkel nagyon sokféle elem elképzelhető. Ezek közül látható néhány a következő képen:

Valószínűleg Tom Jolly is végzett komoly elemzéseket, mert a sok lehetséges elem közül nagyon "jókat" választott. Sajnos nem sikerült kiderítenem, hogy milyen módszerekkel dolgozott. Jolly elemei láthatók a következő képen:

Látható, hogy az eredeti csomóhoz képest jóval üresebbek az elemek. A ketrecen kívül összerakva nem néz ki túl jól, bár lehet úgy forgatni, hogy teljes, hibátlan csomónak nézzen ki.
Az első két elemet még elég könnyű berakni a ketrecbe, de a harmadik már komoly problémát okoz! Az eredeti csomóhoz képest még az is különbség, hogy a 3 elemből kettő itt nem szimmetrikus. Így egyáltalán nem mindegy, hogy egymáshoz képest milyen helyzetben próbáljuk összeállítani őket.
De, ha megtaláljuk az elemek helyes állását, még akkor is komoly nehézséggel kell megküzdenünk! Az első két elem behelyezése után az utolsóhoz még 13-szor kell különböző irányban eltolni az elemeket, hogy végre minden a helyére kerüljön. Vagyis ez a játék 13-as fokozatú! Annak ellenére, hogy mindössze 3 elemet kell a helyére illeszteni. Valószínűleg az egyik legösszetettebb játék ez, ha az elemek egyszerűségét is figyelembe vesszük.
Tom Jolly vizsgálatai nem hozzáférhetők, de (a már többször hivatkozott) Ishino Keiichiro nyilvánosságra hozta az ő számítógépes elemzésének eredményeit. Ezek szerint összesen 10-féle elem alkalmas arra, hogy ketrecbe zárt csomókat készítsünk belőlük. Ezek rajzon:
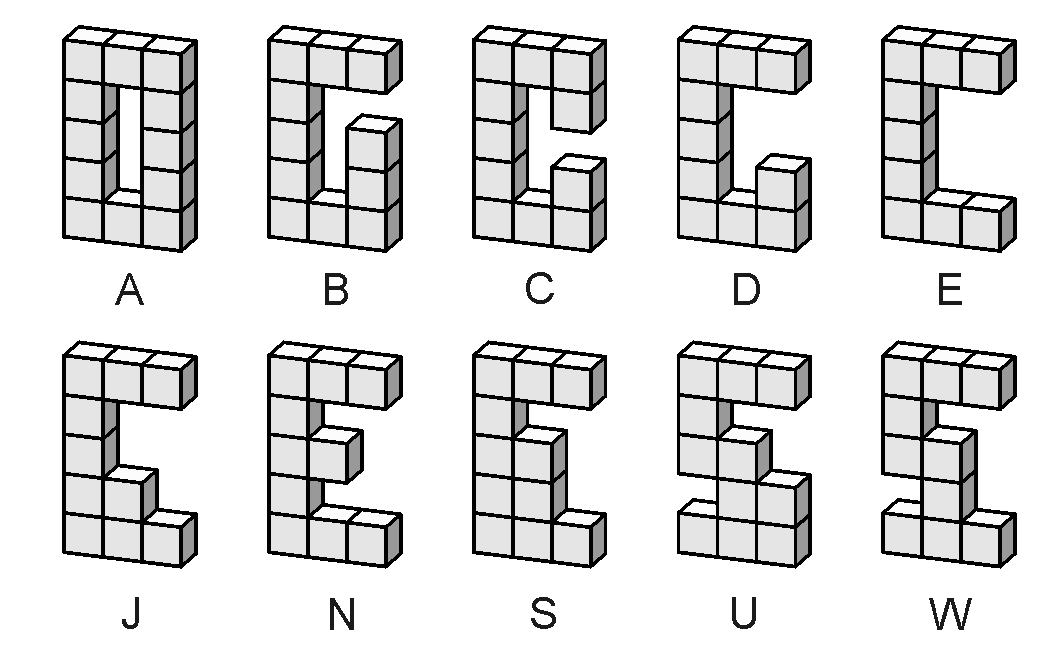
(Azért ilyen hiányos az elemek betűzése, mert elvben más fajták is léteznek, csak azokból nem alkotható csomó.)
Némelyik elem többször is felhasználható. Így, ha az összes lehetséges ketrecbe zárt facsomóhoz szükséges elemkészletet szeretnénk elkészíteni, akkor 18 darab elemet kell csinálnunk. Ezek láthatók a következő képen (egymás mögött azonosak vannak):

Ebből a 18 elemből 79 módon lehet kiválasztani hármat úgy, hogy megoldható legyen a feladvány. E 79 féle készlet közül 35-nek csak egy megoldása van. Ezek jó nehéznek számítanak. Mindössze 8 készletnek van 10-nél nagyobb fokozata, de ezek közül néhány több megoldással is rendelkezik, ami kicsit könnyít a játékon. Mindössze kettő olyan van, aminek 13-as a fokozata és mégis csak egy megoldással rendelkezik, ezek közül az egyik a fent ismertetett Jolly-féle elemkészlet. A másik a két C és egy D elemből álló, így ez egyszerűbb, hiszen vannak benne ismétlődő elemek. Még a legegyszerűbb elemkészlet is 3-as fokozatú, így az sem tekinthető túl könnyűnek.
Ezt a játékot, ilyen teljességgel elkészítve, még soha, senkinél és semmilyen honlapon nem láttam. Ishino Keiichironál szerepel a készlet a lehetséges elemkészletekkel együtt, de csak virtuálisan, számítógépes modell formájában. Ha az olvasó olyan játékot szeretne, ami igazán ritka és tényleg sok, nehéz feladvány létezik hozzá, akkor nagyon javaslom, hogy készítse el ezt! Nem egyszerű, viszonylag pontos munkát kíván, de megéri a fáradságot!