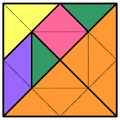
A P pentominó rendelkezik egy érdekes tulajdonsággal, négy darabból elkészíthető önmaga nagyított mása:

Hogy szemléletesebb legyen, ugyanez következzen két rajzon is:

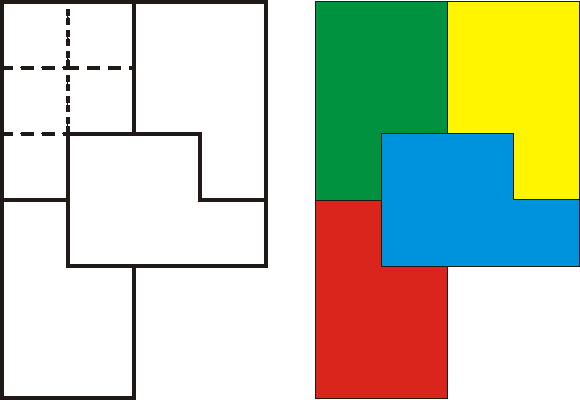
Négy ilyen nagy P-ből összeállítható egy még nagyobb:

És rajzon:

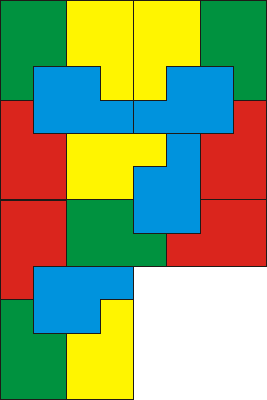
Aztán négy ilyenből egy még nagyobb. (Sajnos csak 61 db fából készült P-m van, úgyhogy a sarkokból el kellett hagynom egyet-egyet.)

A rajz viszont teljes, de lekicsinyítettem az előző ábra méretére:

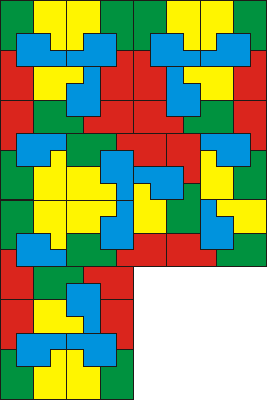
Még néhány fokozat ugyanekkorára kicsinyítve:

A következő:

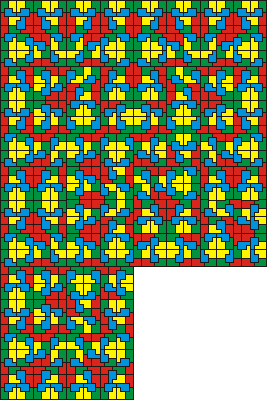
És végül egy 4096 db kis P-ből álló óriási P:

Ezzel a módszerrel a sík tetszőlegesen nagy  részét le tudjuk fedni, más szóval parkettázni (csempézni) tudjuk a síkot.

Az alapos megfigyelő azt is észreveheti, hogy vannak néhányszor ismétlődő mintacsoportok, de minden ismétlődés valahol megszakad. Matematikai precízséggel is belátható, hogy ez a parkettázás hosszabb távon sem eredményez a végtelenségig ismétlődő mintázatot, vagyis nincs olyan eltolás, amivel az egész parkettázás önmagába vihető át. Az ilyen lefedést hívjuk aperiodikus parkettázásnak.

Sokáig az gondolták, hogy ha valamilyen alakzattal aperiodikusan lehet parkettázni, akkor lehet periodikusan is. A P-vel pl. nagyon egyszerűen lehet periodikus parkettázást készíteni:

Aztán az 1960-as évekekben egy nagyon mély matematikai tétel bizonyításakor a kínai-amerikai matematikus Hao Wang és az amerikai Robert Berger megmutatta, hogy van olyan parketta készlet, amivel nem lehet periodikusan lefedni a síkot, aperiodikusan viszont igen. Wang és Berger készlete több mint 20000-féle különböző színes, négyzet alakú parkettát tartalmazott. Felfedezése komoly visszhangot váltott ki, számos matematikus próbálta csökkenteni a szükséges különböző elemek számát. A jelenleg ismert "legjobb" készlet mindössze 13 különböző négyzet alakú elemből áll.

Ha nem ragaszkodunk a négyzet alakhoz, az elemszámot tovább lehet csökkenteni. A - talán legismertebb - aperiodikus parketta készlet Roger Penrose találmánya, mindössze két elemből áll. Ezek láthatók a következő ábrán:

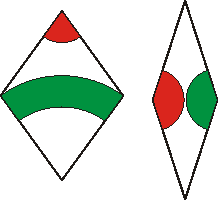
Sajnos, Penrose elemeit színezni kell, és ki kell kötni, hogy csak azonos színek érintkezhetnek. E kikötés nélkül periodikusan is parkettázható lenne a sík velük.

Egy szép ábra egy kis síkrészletről Penrose csempékkel fedve:

(A kép a Wikipedia aperiodikus parkettázással foglalkozó oldaláról származik.)

De térjünk vissza még a P alakhoz! Egy kicsit más arányú P-kkel egyszerűbben is előállíthatunk hasonló parkettázást.

A következő ábra legkisebb P-je hasonló az eggyel nagyobbhoz, az pedig hasonló a kettő összeállításával keletkező még nagyobbhoz. A hasonlóság aránya mindkét esetben ugyanaz a szám. (Ki tudja találni az olvasó, hogy mennyi?)

A 2. és 3. P-ből ismét összeállítható egy még nagyobb P:

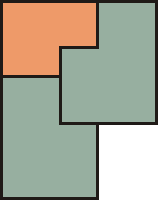
Aztán az utolsó kettőből egy még nagyobb:

És így tovább, mindig az utolsó kettőt összeillesztve, sok lépés múlva kapjuk ezt az ábrát:

Itt is megfigyelhetünk apró, ismétlődő területeket, de belátható, hogy ez a módszer is aperiodikus parkettázást eredményez.

Penrose parkettáit színezni kellett, hogy biztosan aperiodikus legyen a parkettázás, de a  színek helyett lehetne kis füleket, bemélyedéseket is készíteni az elemek oldalára, amiket egymásba kellene akasztani. Ekkor nem lenne szükség színezésre, viszont az elemek alakja nagyon elbonyolódna. Robert Ammann, amatőr matematikus, talált egy konvex, színezés nélküli elemkészletet, amivel csak aperiodikusan lehet parkettázni. A készlet mindössze 3 elemből áll, ezek láthatók a következő ábrán:

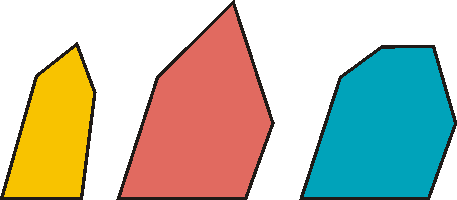
Nagy örömömre, én rendelkezem egy viszonylag nagy készlettel ezekből az elemekből. Nagyon érdekes és egyáltalán nem könnyű velük "parkettást" játszani! A következő képen az én készletemből összeállított alakzat látható (a gyufásdoboz a méretek érzékeltetése miatt került a képre):

Befejezésül még egy, kevésbé szabályos forma az Ammann parkettákból: