Öt négyzet összeerősítésével keletkeznek a pentominó elemek. Ezekből 12 féle létezik, ami nagyjából elég egy se nem könnyű se nem túlságosan nehéz játékhoz. Ha hat négyzetet erősítünk össze teljes oldaluknál, akkor a hexominó elemeket kapjuk:

Talán első látásra nem világos minden esetben a 6 négyzet elhelyezkedése, ezért a szemléletesség kedvéért következzenek rajzban is az elemek:

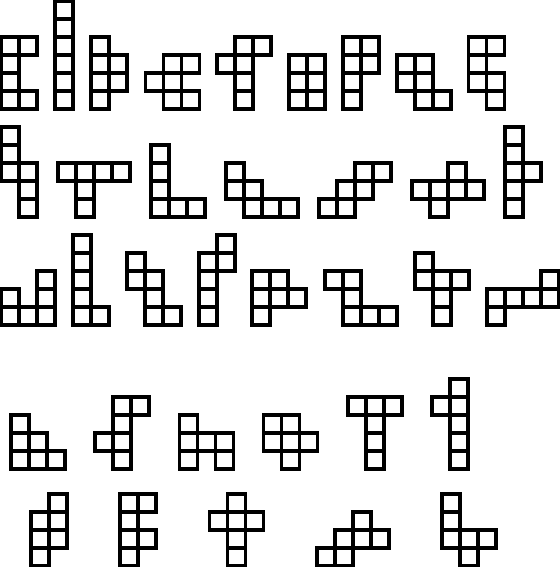
A 35 féle elem közül némelyek egész egyszerűek (pl. az első sor téglalapjai). Van néhány tengelyesen szimmetrikus (pl.  a 4. sor első eleme), van ami középpontosan szimmetrikus (pl. a 3. sor utolsó eleme), de a legtöbb elem semmilyen szimmetriával nem rendelkezik. Aki sokat játszik hasonló kirakókkal, az már biztosan tudja, hogy a nem szimmetrikus elemek okozzák a legtöbb bosszúságot :)

A 35 elem összesen 210 négyzetből áll. 210 négyzetből sokféle téglalap készíthető: 2×105-ös, 3×70-es, 5×42-es, 6×35-ös, 7×30-as, 10×21-es és 14×15-ös. A geometriához kapcsolódó játékoknál nagyon gyakori feladvány egy téglalap vagy négyzet vagy valamilyen szabályos figura kirakása. Vajon ezen téglalapok közül némelyek összeállíthatók a hexominó elemekből? Ha igen, melyikek és hogyan?

Könnyű észrevenni, hogy a 2×105-ös túl keskeny, abba nem fér bele pl. az első sor 4. eleme. Talán még a 3×70-es esetén is belátható egyszerű formai meggondolásokkal a a kirakás lehetetlensége. De mi a helyzet a többi téglalappal? Mielőtt nekiállunk az elemeket pakolászni, érdemes egy kicsit elgondolkodni!

Színezzük ki sakktábla szerűen a téglalapokat! Mindegyik páratlan sok (pontosan 105) sötét és világos mezőt fog tartalmazni, akárhogy kezdjük is a színezést. Például a 14×15-ös:

És most az elemeket is színezzük ki! Ezt már nagyon sokféleképpen meg lehet tenni, íme egy mód:

De akárhogy színezzük is az elemeket, azt tapasztaljuk, hogy a vonal felettiek 3 sötét és 3 világos mezőt tartalmaznak, a vonal alattiak pedig 2-t illetve 4-et (tehát páros sokat). A vonal fölött 24 elem helyezkedik el, 24×páratlan az páros. De a téglalapban meg páratlan sok sötét mező volt! Ezért biztosan nem lehet lefedni az — összesen páros sok sötét mezőt tartalmazó — elemekkel a téglalapokat!

A fenti gondolatmenet sok "játék"-ra és kirakási problémára alkalmazható. Néha azért kicsit ravaszabbul kell színezni :) Fontos megjegyezni, hogy fordítva nem igaz ez az okoskodás! Attól, hogy színezésekkel nem jutunk ellentmondásra, még nem biztos, hogy egy alakzat kirakható!

"Sajnos" téglalap tehát nem rakható ki az elemekből. De majdnem téglalap igen! Ha megengedjük, hogy egy négyzet kilógjon, akkor máris található megoldás:

Egy ilyen feladvány azonban elképesztően nehéz! Számítógépes programokkal is általában több nap egy megoldás megtalálása, a feladat teljes kielemzése pedig akár hónapokat is igénybe vehet. Elképzelhető, hogy az emberi intuíció gyorsabban is talál megoldást, de ahhoz vagy nagy szerencse kell, vagy valami általam ismeretlen képesség :) Én nem tudom megoldani az ilyen bonyolultságú játékokat! Játékboltokban lehet kapni több ezer darabos "puzzle"-kat, azok megoldása nem szokott gondot okozni, de ez a 35 elem rendre kifog rajtam! Azoknak a játékosoknak javaslom a teljes hexominó készletet, akik szeretik az extrém nehéz feladványokat ráadásul hatalmas türelemmel rendelkeznek!

Ha a teljes készlet sokaknak megoldhatatlanul bonyolult is, számos érdekes részhalmaza létezik az elemeknek, amikkel az egészen könnyűtől a még megoldható nehézségűig sok-sok feladvány alkotható! Ezekről későbbi bejegyzésekben lesz szó.

Befejezésül álljon itt még két alakzat az összes elem felhasználásával!

Egy lyukacsos téglalap:

És egy bástya:

Az elemeket egy körtefa rönkből készítettem, azért ilyen szép a fa mintázata!