Napjaink egyik legnépszerűbb fejtörő játéka a Sudoku. Olyanok is nagy kedvvel fejtik, akik semmi más gondolkodni valót nem szeretnek, sőt megriadnak egy kis töprengéstől. Nem véletlen, hogy a Sudoku megihlette az ördöglakat-tervezőket is. Az egyik legötletesebb változatot Nob Yoshigahara alkotta meg. Nob Yoshigahara neve már sokszor előfordult a blogon, az egyik legnagyobb alakja az ördöglakatok világának. Nem véletlenül van róla elnevezve a játéktervező verseny.
Bár az eredeti Sudokut 9×9-es táblán játsszák, Yoshigahara verziója mindössze 5×5 vagyis 25 négyzetből áll. Számok helyett pedig színeket kell elhelyezni úgy, hogy semelyik sorba és oszlopba ne kerüljenek azonosak. Ezt a változatot nem papíron ceruzával kell játszani, hanem pl. fából elkészített játékelemekkel. Az ördöglakatos változatban a csavar az, hogy bizonyos színek össze vannak erősítve:

Ezt a 9 elemet – 7 triominót és 2 dominót – kell elhelyeznünk úgy, hogy egy 5×5-ös négyzetet alkossanak és semelyik sorban, oszlopban ne szerepeljenek azonos színek. Yoshigahara a Fifth Avenue nevet adta játékának. Apró kockákból elkészített változata Alan Boardman cserejátéka volt az 1998-ban megrendezett 18. IPP-n. Alan Boardman a miniatúrák mestere, az egész játék elfért egy 25×25×5 mm-es dobozban.
A következő képen "majdnem sikerült" megoldani:

Az első és utolsó oszlop jó, de sem a többi oszlop, sem a sorok nem megfelelőek.
A játékot én kis natúr kockákból készítettem el. Ezeket pácoltam, majd a színezett kockákat ragasztottam össze. Mutatok egy fotót az alapanyagokról. Hátul látható a játék megoldva, szándékosan életlen, hogy ne lehessen kivenni az elemek elhelyezkedését:

Nem egyszerű ilyen kockákat beszerezni... De ehhez a játékhoz nincs szükség hatalmas pontosságra, sem szépen letört élekre, így kevésbé kidolgozott alapanyagokból is meg lehet próbálni elkészíteni. Sőt, később egy letölthető változatot is szerepeltetek.
El kell árulnom, hogy én nem boldogultam ezzel a játékkal. Igaz, hogy nagy sudokus sem vagyok, de abból azért az egyszerűbbek nem okoznak gondot.
Egy kicsit elgondolkodtam, hogy mi is okozza e játék nehézségét. Először megvizsgáltam, hogy egyáltalán hány módon lehet kirakni ilyen alakú elemekből az 5×5-ös négyzetet. Erre van könnyen hozzáférhető, remek program, a BurrTools. Néhány lényegesen különböző megoldás látható a következő ábrán:
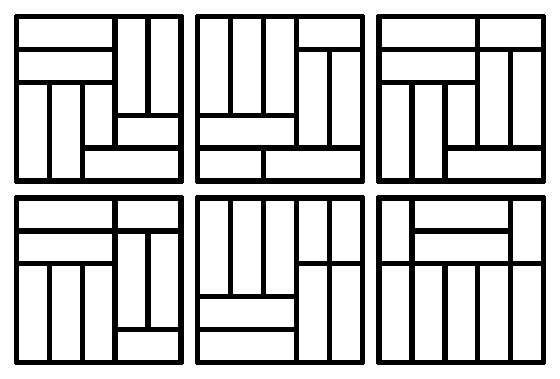
Összesen 24 megoldás létezik, ami elsőre nem hangzik vészesen soknak. Azért nem egyszerű megtalálni a ténylegesen különbözőket, de ez még nem reménytelen. De vizsgáljunk egy konkrét megoldást! A színezés miatt minden elem különböző. Így egy megoldásban a 7 triominót 7! = 5040 módon lehet elrendezni, a 2 dominót pedig 2-féleképpen. Az eddig: 5040×2=10080. Egyik elem sem szimmetrikus, így mindegyik 2-féleképpen állhat, vagyis, ha csak az elemeket forgatjuk egy adott elrendezésben, akkor 29=512 különböző mintázatot kaphatunk. Ez összesítve: 10080×512=5160960 különböző mintázat. És már írtam, hogy 24 elrendezés létezik, vagyis összesen 5160960×24=123863040 különböző módon lehet ezekből az elemekből kirakni az 5×5-ös négyzetet. Több mint 100 millió! Gondoltad volna?
Vajon ezek közül az elrendezések közül hány jó? Vagyis hány olyan van köztük, ahol nincs színegyezés? És itt látszik Yoshigahara zsenialitása, mert mindössze egyetlenegy a megfelelő. Vagyis a játékban a 100 millióból kell megtalálni az egyet! Így már nem is tűnik olyan könnyűnek.
Az még hozzátartozik a játék történetéhez, hogy Yoshigahara 1984-ben találta fel. Bár a Sudoku már 1976-ban megjelent, de Japánba csak 1986-ban ért el. Lehet, hogy nem is ez ihlette? 1984-ben még nem volt minden háztartásban számítógép, valószínűleg nem volt egyszerű elvégezni a játék elemzését. Nem tudom, hogy Yoshigahara akkora zseni volt-e, hogy számítógép nélkül tervezte a játékot, de valószínűsítem, hogy nem, ő is használt programokat.
Amikor szembesültem ezzel a hatalmas variáció mennyiséggel, elterveztem, hogy kitalálok egy hasonló, de kicsit egyszerűbb játékot. Én a 4×4-es táblát, 4 színnel céloztam meg. Olyan alakú elemeket kerestem, hogy viszonylag sok jó elrendezés legyen. Én is 3 és 2 kockából álló elemekben gondolkodtam, ezekből nincs túl sokféle, mindössze a következők:
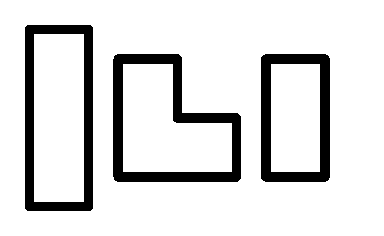
Sokat kísérleteztem, végül arra jutottam, hogy az lesz a legjobb, ha mindhárom elemből 2-2 darabot használok. Így viszonylag sok lehetséges elrendezést kapok, összesen 30-at. Ezek közül néhány:

Most már csak ügyesen ki kell színezni az elemeket, hogy legyen is megoldás, de ne sok. A következő képen láthatóig jutottam:

Ezeknek az elemeknek van egy különlegessége, ami előny is lehet, de hátrány is. A két L alakút nem feltétlenül elég síkban forgatni, az összes állásukat csak úgy kapjuk meg, ha a térben is átforgatjuk őket. Egyelőre nem készítettem el fából, csak a modellező készletemből, mert valószínűleg lesz ennél jobb. Ugyanis akárhogy próbálkoztam, nem sikerült olyan színezést kitalálnom, aminek csak egy megoldása van. Ezekkel az elemekkel 3 különböző jó négyzetet is ki lehet rakni. Az egyik:

Azért nem olyan könnyű ez sem. Szerencsére lerajzoltam a megoldást, mert jól el kellett gondolkodnom, amikor újra össze akartam rakni :)
De nézzük meg most is, hogy hány lehetőségből kell a jókat megtalálni.
Minden elemből kettő van, így a sorrendjük 2×2×2 = 8 lehet. Minden elem állhat "felfelé és lefelé" az 26=64. És 30 elrendezés létezik. Ezért az összes lehetőségek száma: 8×64×30=15360. Azért ez messze van a 100 milliótól! Ráadásul nem is egyedi a megoldás. (Még foglalkozom a kérdéssel, lehet, hogy találok jobbat. De az olvasót is biztatom, más elrendezések és színezések keresésére, hátha sikerül ennél nehezebbet találni!)
Készítettem egy letölthető változatot az elemekről. Aki nem tudja fából, vagy esetleg LEGO-ból elkészíteni, az nyomtassa ki, vágja darabokra és próbálkozzon az összerakással. Érdemes. A PDF letölthető innen.




