Régebben volt szó a Sudoku és a kirakó játékok kapcsolatáról ebben a bejegyzésben. (Aztán felhívták a figyelmemet, hogy ezek latin négyzetek, a sudokuban sokkal több mindennek kell megfelelni.)
Egy nagyobb projekt kapcsán most újra elővettem ezt a játéktípust és jópár feladványt készítettem hozzá. Ezek közül párat lehetett elkészíteni az Ördöglakat Találkozón.

Amint a képen is látható, a színes elemek összeállíthatók egy négyzetté úgy, hogy minden sorban és oszlopban csupa különböző szín szerepel. Az ilyen elrendezéseket hívjuk latin négyzeteknek.
Egyáltalán nem nehéz olyan elemeket találni, amikből kirakható latin négyzet. Ha kiszínezünk "jól" egy négyzetet, akkor azt felbonthatjuk elemekre. Az viszont egyáltalán nem biztos, hogy az így kapott elemeknek csupán egy elrendezésük lesz helyes. A fenti kép elemeivel több tíz módon lehet latin négyzetet összeállítani.
Sokkal nehezebb olyan elemeket találni, amikkel csak egyetlen módon lehet latin négyzetet kirakni, és ezek lesznek az igazán érdekes játékok. Az is látszik a képen, hogy minden elem egy kis egyenes léc színezésével jön létre. Ez nagyban megkönnyíti az előállítást, csak méretre kell vágni egy hosszabb lécet, valahogy színes pöttyöket készíteni rá és már játszhatunk is. Lehetnének L alakú elemek is vagy akár még bonyolultabbak, de ennek a játéknak az egyik szépsége, hogy még így is jó nehéz feladványokat lehet készíteni.
Vizsgáltam az összes 2 vagy 3 egység hosszú elemet, amiken négyből 3 különböző szín található. Összesen 18 ilyen elem létezik. Ezek közül 4 db 3 egység hosszút és 2 db 2 egység hosszút 7425 módon lehet kiválasztani. Ezen készletek közül 96-nak csak egy megoldása van. Egy ilyet láthattok következő képen:
Készítsétek el akár fából, akár papírból! Egyáltalán nem egyszerű, de nem is beláthatatlanul nehéz kirakni ebből egy latin négyzetet.
Mivel minden elem alakja szimmetrikus, ezért a másik oldaluk üresen maradhat.
Vagy még jobb, ha a másik oldalára egy másik színezés készül. Ezt javaslom:

Tehát az A elem hátán a J, a B elem hátán az L és így tovább.
Mind az ABDGOR elemeknek, mind a JLEHMP-nek egy megoldása van. Így rögtön olyan készletet kapunk, amivel 2 feladványunk is lesz.
Sőt, lehet úgy is kombinálni az elemeket, hogy néhányat az egyik oldalból fordítunk felülre, néhányat meg a másikból. Összesen 64 lehetőségünk van ilyen forgatásokra, ebből 8 db olyan van, aminek szintén csak egy megoldása létezik. Ez a 8 (a fentieket is beleszámolva):
ABDGOR, ABDHOR, BEGJMR, ADHLMR, BEGJOP, ADHLOP, DHJLMP, EHJLMP
Ha nem ragaszkodunk az egy megoldáshoz, akkor még 12 megoldható elemkészletet kapunk:
BDGJOP, BEHJOP, ADGLOP, AEHLOP, BDGJMR, ADGLMR, BEHJMR, AEHLMR, BDHJOP, AEGLMR, BDHJMR, AEGLOP
Az első fotón az AEGLMR kombináció egyik megoldása látható. Ez az elemkészlet a legkönnyebbek közül való.
Összefoglalva:
Ha elkészítjük ezt a 6 db kétoldalas elemet, 20 feladványt kapunk, a viszonylag nehéztől kezdve a lényegesen könnyebbekig. Nagyon javaslom!
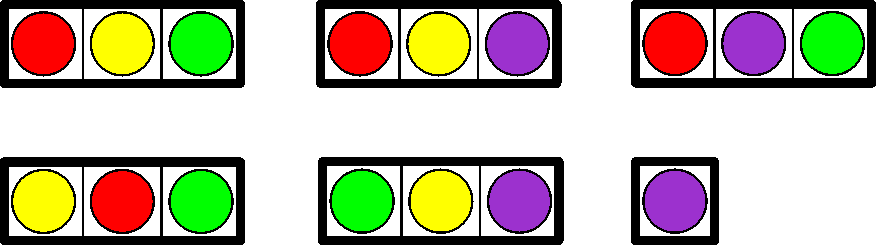
Egy kicsit (talán) könnyebb feladványt kapunk, ha nem használunk 2 egység hosszú elemet, csak 5 db 3 egységnyit és 1 db egy egységnyi négyzetet. Ennek az elemkészletnek 2 megoldása is létezik:
Ha viszont nehezebb feladványra vágyunk, akkor érdemes az 5×5-ös négyzetek között keresgetnünk. Szintén csak egyenes elemekből áll a következő elemkészlet is, de tartalmaz egy 2×2-es négyzetet.
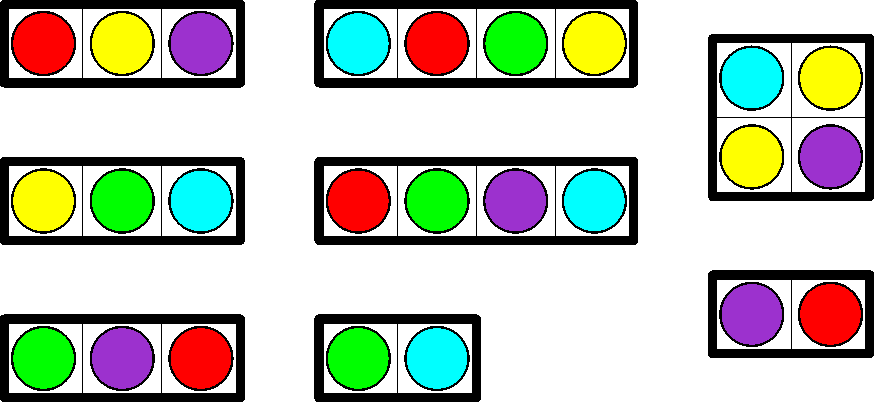
Ez egy jó bevezetés lehet az 5-ös latin négyzetek világába. Igazán komoly erőpróba, de mégsem annyira nehéz, mint a sudokus bejegyzésben bemutatott Fifth Avenue.




