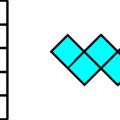
Hát, ez könnyű! Mindenki tud pár négyzetből összeállítani kisebb-nagyobb téglalapokat, pl. két négyzet egymás mellett máris egy 1×2-es téglalapot alkot. Nehezítsük a feladatot! Először néhány négyzetet erősítsük össze egy elemmé, majd az így kapott elemeket használjuk! Így már sokkal érdekesebb problémákkal találkozhatunk.
Öt négyzetből készíthetünk egy L alakú formát (L pentominót). Ebből az L-ből sem nehéz különböző téglalapokat kirakni. A következő képen egy 8×10 egység oldalú látható:

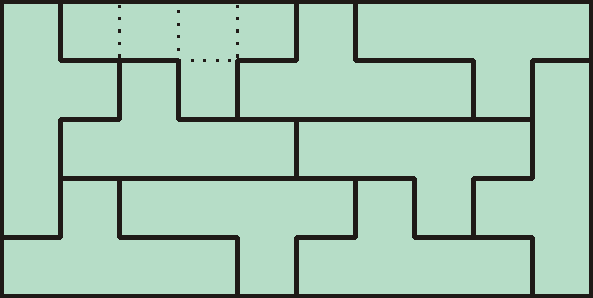
Látható, hogy a nagy téglalap kisebbekből, 2×5-ösökből áll össze. Vajon csak így lehetséges? Minden L pentominókból kirakható "nagy" téglalap felbontható kisebb, 2*5-ös téglalapokra? Ebből következne, hogy minden, L-ekből kirakható téglalap egyik oldala páros. Ki lehet-e rakni olyan téglalapot, aminek mindkét oldala páratlan?
A válasz pozitív, mint ahogy a következő képen is látható:

A fent látható 9×15-ös téglalap biztosan nem bontható fel 2×5-ösökre az L-ek más elrendezése esetén sem.
Olyan téglalapot, aminek mindkét oldala páratlan hosszúságú, és kirakható L pentominókból, David Klarner amerikai matematikus talált először. Egy 1969-es cikkében közölte a 9×15-ös elrendezést. Furcsa, hogy ennél kisebb, hasonló tulajdonságokkal rendelkező téglalap is létezik és erről nem tesz említést Klarner! Nem könnyű megtalálni, de nem is reménytelenül nehéz vállalkozás! Megpróbálkozik vele az olvasó? (Akár egy négyzetrácsos papíron rajzolgatva is rá lehet bukkanni a megoldásra!) Nem árt előbb elgondolkodni azon, hogy egyáltalán mekkora téglalapok jöhetnek szóba!
A L pentominóból kirakható téglalapok közül csak a 2×5-ös és a feladványként keresett páratlan oldalszámú a "lényeges". Az összes többi előállítható ezek kombinációjából. Így ezt a két téglalapot tekinthetjük az L pentomínó alap "építőelemeinek" vagy - matematikaiasabb nyelven szólva - prím tégláknak. (A prímszámokból előállítható az összes természetes szám, hasonlóan a prím téglákhoz, ezekből az összes téglalap rakható ki.)
Nagyobb változatosságot mutat az Y pentominó. Ebből már a legkisebb kirakható téglalap összeállításához is kell némi gondolkodás:
A következő képen látható 17×15-ös téglalap már elég nehéz feladvány:
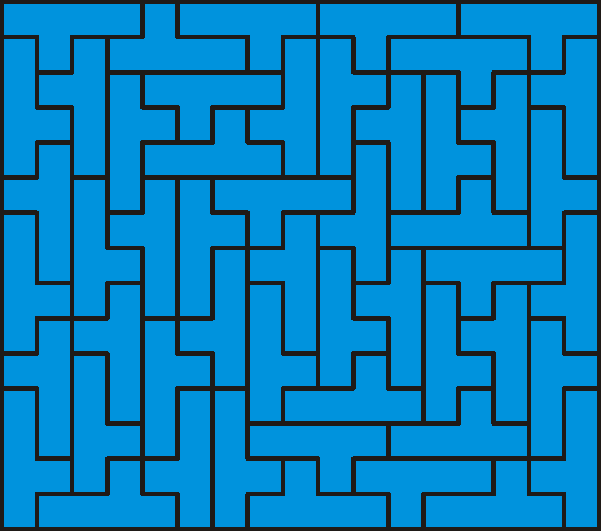
A két méret között is vannak kirakhatók! Megpróbál az olvasó ilyet találni? Sőt egy négyzet is kirakható az Y pentominóból, még az is kisebb, mint a fenti 17×15-ös téglalap.
Néhány négyzetekből összeállítható alakzatról nagyon nehéz eldönteni, hogy egyáltalán kirakható-e belőlük téglalap. És nem is kell nagy alakzatra gondolni! Pl. a mindössze 6 négyzetből álló Y hexominóról:
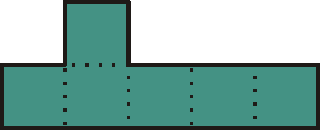
csak nagyon sokára, 1989-ben derült ki, hogy kirakható belőle téglalap. Ennek megkísérlését csak a nagyon kitartó olvasóknak javaslom! 92 elemet kell felhasználni, így alakítható ki belőle a legkisebb, 23×24-es téglalap! Ez látható a következő fotón:

Következzen még néhány érdekes, nem beláthatatlanul nehéz téglalap kirakás!
A P alakú, 7 négyzetből álló alakzatból (P heptominóból):
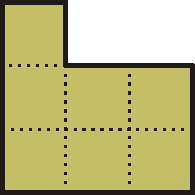
sokféle téglalap kirakható. Következzen a legkisebb, páratlan sok elemet tartalmazó, ami 15×21 egység oldalú, így 45 heptominóból áll:

Ugyanezekből az elemekből jóval kevesebb darabból összeállítható páros oldalhosszúságú téglalap. Próbálja megkeresni az olvasó!
A 6 négyzetből álló (hexominó) alakzatból:
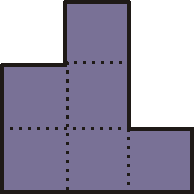
20-nál kevesebb is elég egy téglalap összerakásához. Sikerül?
Végül álljon itt egy másik, nagyon nehéz feladvány! A következő, hét négyzetes alakzatból:
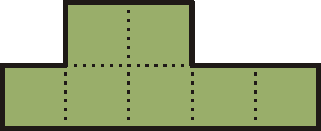
76 darab szükséges a lehetséges legkisebb téglalap összerakásához: