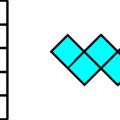
A legjobb, ha mindkettő!

Egy véletlenül elcsípett beszélgetésből díjnyertes játék lett. Ennek történetéről és a játék egy lehetséges megvalósításáról szól ez a bejegyzés.

Ha papírból szeretnénk kockát hajtogatni, többféle hálóból indulhatunk ki. Érdekes feladvány megtalálni az összes olyat, ami csak négyzetekből áll! 11 ilyen létezik, ezek láthatók a következő ábrán:

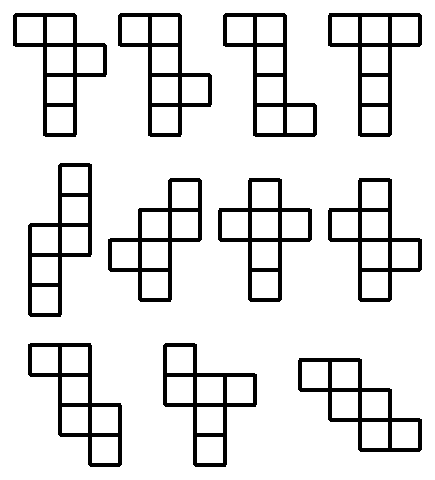
(Hm, most jutott eszembe: akár ez a 11 alakzat is alkalmas lenne egy kirakójátékhoz. Egy későbbi bejegyzésben visszatérek rá.)

Ha már egy kocka is ilyen sokféle hálóval rendelkezik, akkor mennyi lehet két, három vagy négy kockából álló alakzatoknak? Rengeteg!

Két kockából álló alakzat csak egy van: 

Három kockából már kétféle test rakható ki:

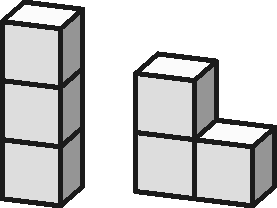
Először George Miller, amerikai játéktervező kezdett el gondolkodni azon, hogy vajon van-e olyan háló, amiből mindkét test előállítható hajtogatással. Hosszas kísérletezésbe kezdett, és nagy örömére talált is egyet. Meg volt győződve róla, hogy az egyetlen lehetséges megoldást fedezte fel. Egy kiállításon büszkén mesélte valakinek eredményét. A közelben állt és hallotta a beszélgetést Donald Knuth (igen, az a Knuth, a számítástudomány, az algoritmuselmélet ma élő egyik legnagyobb alakja, a "Számítógép-programozás művészete"  c. könyv szerzője). Akkor nem szólt semmit, de pár hét múlva levelet kapott Miller, amiben leírja Knuth, hogy nagyon tetszett neki a probléma és "kicsit" megvizsgálta kérdést. A feladatnak egyáltalán nem csak egy megoldása van, hanem egész pontosan 29026. Ezek közül pár, érdekeset be is mutat Knuth.

De még jobban tetszett neki a négy kockából álló testek hálója. Ilyen test nyolcféle létezik:

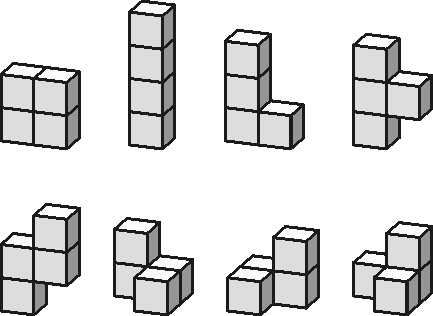
(Ismerősek ezek a testek? A Szóma kockánál volt már szó róluk! )

A bal felsőt kivéve az összesnek 18 oldallapja van. Így felvethető a kérdés, hogy vajon létezik-e közös hálójuk. Knuth, megvizsgálva a minden test több millió (sőt, százmillió) hálóját, talált 68 olyan elrendezést, amiből az összes kihajtogatható.

Ezek közül az egyik - minden szempontból megfelelő - hálót kiválasztva gyorsan megszületett George Miller és Donald Knuth közös játéka, a "Cubigami". Miller foglalkozott a gyakorlati problémákkal, Knuth pedig az elméleti hátteret biztosította. A játék célja egyszerűen megfogalmazható: hajtogatással készítsük el az összes 4 kockából álló alakzatot (kivéve a 2-szer 2-es "négyzetet"). A Cubigami 2005-ben elnyerte a zsűri különdíját a logikai játékok nemzetközi találkozóján.

Évek óta tudok a játékról, nagyon tetszett már akkor is, amikor először olvastam róla. Sajnos nem lehetett hozzájutni. Elkészítettem papírból, de úgy nem volt igazán jól használható. Már-már kezdtem lemondani róla, amikor egy játékbolt kirakatában megpillantottam egy kisgyerekeknek szánt összerakós építőjátékot. Rögtön láttam, hogy ebből elkészíthető a Cubigami. Vettem is egy kisebb készletet és a kezdeti elrontott próbálkozások után, azt hiszem, megtaláltam a megoldást.  Az első képen az altalam készített példánnyal játszik a fiam.

Ime a kiterített háló:

Látható, hogy bizonyos összeköttetések csavarral vannak megerősítve:

Annyira, hogy a csavarok be is vannak ragasztva egy-egy elembe. Az így kapott kötés  forgatható maradt, de nem bontható. Talán nem a legszebb megoldás, de tökéletesen működik. (Időközben láttam meg, hogy az eredeti Cubigami most már kapható, kicsit jobban néz ki, mint az én verzióm :))

Miután elkészült a játék, körülbelül fél nap alatt sikerült mind a hét testet kihajtogatni. Íme:

Remek szórakozás volt. Megjegyezni persze nem tudtam a hajtogatás menetét, így amikor legközelebb ismét megpróbálom, újra rá kell jönni mindenre!