Az IPP-re mindenképpen szerettem volna olyan játékokat is vinni, melyeknek van magyar vonatkozása azon kívül is, hogy én készítem el őket. Játékos körökben a bűvös kockáról mindenki tudja, hogy magyar találmány, de valami másra is szerettem volna felhívni a figyelmet. Lehetett volna matyó mintás ördöglakatot készíteni vagy a csikós-puszta-Puskás vonalon haladni, de én legalább ennyire büszke vagyok a szellemi-tudományos teljesítményeinkre. Ezért néhány játékomban az egyik leghíresebb magyar matematikusnak Bolyai Farkasnak állítottam emléket.
Bolyai Farkasról sokaknak csak annyi ugrik be, hogy János apja volt. Kevesen tudják, hogy egy nagyon szép és könnyen érthető matematikai tétel ma is az ő nevét viseli. A Bolyai tétel szerint: "Minden azonos területű sokszög véges sok vágással egymásba darabolható."
Az igazsághoz tartozik, hogy Bolyai Farkassal nagyjából egy időben mások is bebizonyították ezt az állítást, így a nemzetközi irodalom gyakran Bolyai–Gerwien- vagy Wallace–Bolyai–Gerwien tételként említi.
A tétel annyira szemléletes, hogy szinte kiált az ollóért és papírért, pár sokszöggel nagyon egyszerűen szemléltethető. Én ennél egy kicsit komolyabb kivitelre törekedtem, és próbáltam arra is ügyelni, hogy viszonylag kevés elemből álló, érdekes formák szerepeljenek a játékokban.
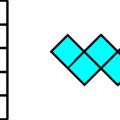
Ezen megfontolásokból készült néhány "Könyvfejtörő". Például a négyzet szabályos hatszöggé való átdarabolhatóságát szemléltető:

A könyvecske bal oldalán egy kártyán rövid leírás található a játékról. A kártya hátulján szerepel a megoldás. A könyv becsukva gumival zárható, így nem esnek ki az elemek. Már többször bemutattam hasonló játékkönyveket, de talán most jutott el arra a szintre, hogy nemzetközi porondon is meg mertem mutatni.
E blog szokásaitól eltérően most következzenek a megoldások is, hogy látni lehessen, mennyire szép és egyszerű a két alakzat kirakása:

A játékban látható átdarabolás a ma ismert legjobb. Nem tudjuk, hogy létezik-e ennél kevesebb darabból álló megoldás.
Az IPP-n is többen kérdezték, hogy ez a megoldás matematikailag korrekt-e, nincs-e benne valahol egy kis csalás, nem lehet-e, hogy a látszólag egy egyenesbe eső oldalak mégis egy kis szöget zárnak be, vagy a derékszög mégsem teljesen derékszög.
Nos, a megoldás teljesen korrekt (amennyire persze egy fából kivágott játék pontos lehet.) Körzővel, vonalzóval, matematikai értelemben pontosan is megszerkeszthetők ezek az elemek és tényleg mindkét alakzatot kiadják.
Talán még furcsább, a görög kereszt átdarabolása szabályos háromszöggé! A játék:
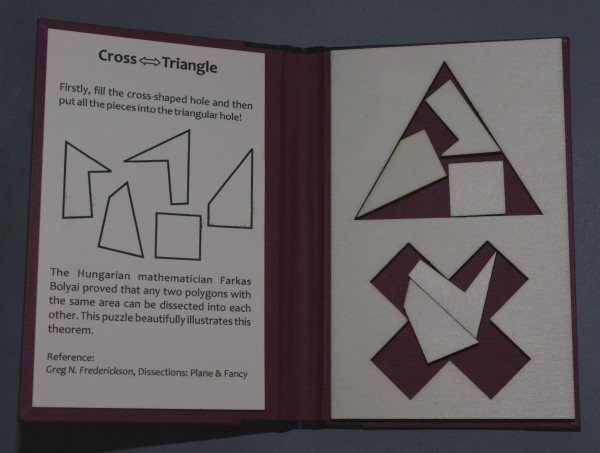
És a megoldások:

Ez a megoldás szintén a ma ismert legjobb, legkevesebb elemből álló. És ismétcsak teljesen korrekt matematikai értelemben.
Mindkét eddig bemutatott játék viszonylag könnyű. Kisebb gyerekek vagy a fejtörők iránt nem nagyon lelkesedők is hamar eredményre juthatnak bennük. (Nehezebbé válnak, ha a kirakandó alakzatok körvonalát nem adjuk meg, hanem pl. az elemeket a könyvből kivéve az asztalon kell összeállítani a különböző formákat.)
Érdekes, hogy mindkét játék 5-5 elemből áll. Bár léteznek nagyon nehéz 3, 4 vagy 5 darabos fejtörők, (pl. az Ex-3), de ez nem tartozik közéjük. Az IPP-n hamar elkapkodták az összes példányt, de nem hiszem, hogy a viszonylagos könnyűsége miatt. Talán inkább azért, mert kicsiknek is játszható, sőt felhasználható az oktatásban?
Bolyai tétele két sokszög egymásba darabolásáról szól, de könnyen általánosítható, hogy több sokszög eggyé darabolásáról szóljon! Erre is készítettem egy példát. A következő játékban 3 kis négyzetet kell egy nagyobbá alakítani:

Ez már nem egyszerű játék! A 3 kisebb négyzet kirakása még csak-csak sikerül a legtöbb próbálkozónak, de a legnagyobbé bizony komoly fejtörést kíván. Úgyhogy e játéknál csak az egyszerűbb rész megoldását adom meg:

Próbálkozzon az olvasó a nagy négyzet kirakásával!
A három négyzet egy négyzetté való átdarabolása nagyon sok speciális esetre osztható. Máshogy kell az elemeket megszerkeszteni, attól függően, hogy milyen a kicsi négyzetek aránya. Erre a problémakörre korántsem mondhatjuk, hogy ismerjük a közel optimális megoldást. Elképzelhető, hogy bizonyos esetekben az itt bemutatottnál egyszerűbb átdarabolások is létezhetnek. Érdekes feladvány ilyenek keresése!
Bár nem könyv formátumban, de még régebben elkészítettem az egyik leghíresebb átdarabolást játék formájában. Ebben egy szabályos háromszög alakul át négyzetté.
A háromszög:

És a négyzet:

A játék külön érdekessége, hogy némely elemeket egymáshoz is lehetne rögzíteni egy csuklós pánttal, csak e körül kell elforgatni őket. Az animáció ezt szemlélteti:

Hogy hogyan lehet ilyeneket kitalálni? Hát, fogalmam sincs. Valószínűleg kicsit zseninek kell lenni hozzá, mint amilyen Henry Dudeney is volt, aki (többek közt) ez utóbbi átdarabolást is megalkotta.
Azért vannak módszerek, amikkel viszonylag egyszerűen meg lehet találni alakzatok egymásba darabolását. Ezek általában nem adnak optimális eredményt, de szemléletesek és könnyen megszerkeszthetők. Egy ilyen módszert mutatok most be, de csak nagyon nagy vonalakban.
Tegyük fel, hogy két kisebb négyzetet szeretnénk átdarabolni egy nagyobba! (Természetesen a nagyobb területe megegyezik a két kisebb összegével.)
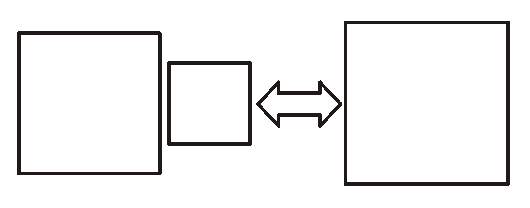
A két kisebb négyzetből összeállíthatunk egy ismétlődő mintát, amivel akár az egész síkot lefedhetnénk:

Ha ebben az ábrában összekötjük a nagyobb négyzetek középpontjait:
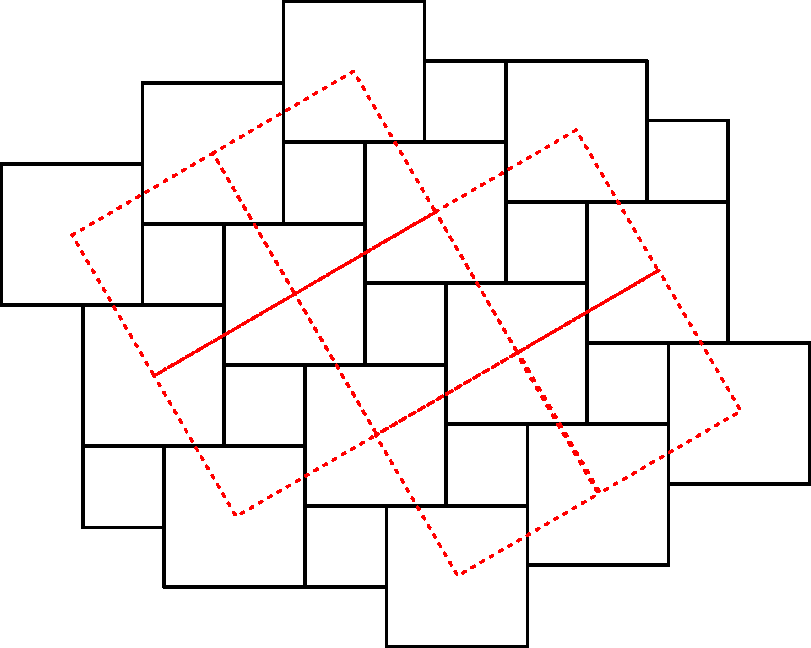
akkor pont a legnagyobb négyzeteket kapjuk meg! És egy piros négyzeten belül kialakult az az 5 alakzat, amiből a nagy négyzet is és a két kicsi is kirakható.
A szorgalmas olvasónak ismerősek lehetnek ezek az alakzatok. Nagyon hasonlókkal találkoztunk már egy régebbi játéknál, a Perigal négyzeténél. Ugye, hogy minden mindennel összefügg?