Ugye mindenkinek van otthon egy rakás pentominója meg jónéhány tetrominója és a társai? Mert a most következő játékokhoz egy készlet nem elég, de még kettő sem. Szerencsére nekem van pár:

A pentominókról már sokszor volt szó a blogon, nem véletlenül, szerintem az egyik legsokoldalúbb játék. A kb. 100 éves történelme számtalan könnyebb és máig megoldatlan problémát rejt, így gyerekek, de akár tudósok is foglalkozhatnak a témával. Érdemes elolvasni az előbb linkelt bemutató bejegyzést, az ott szereplő elnevezéseket fogjuk használni itt is. A most bemutatandó feladványok között lesz egész egyszerű is, de ismeretlen megoldást is keresünk!
A pentominók általában egyáltalán nem felcserélhetők, azon kívül, hogy mindegyik öt négyzetből áll, nem sok közös tulajdonságuk van. Van köztük tengelyesen szimmetrikus, 1, 2, 4 tengellyel, van középpontosan szimmetrikus és van, amelyiknek egyáltalán nincs szimmetriája. Nagyon érdekes problémák azok, amelyekben egy semmilyen szimmetriával nem rendelkező elem ugyanolyan szerepet tud betölteni, mint egy "nagyon szimmetrikus". De mi is lehet ez a szerep?
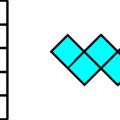
A következő ábrán ugyanaz az alakzat látható F-ekből és W-kből kirakva:

Nem is kellett a kirakáshoz sok darab, mindössze kettő mindkét fajta elemből. Azonban nem mindig ennyire egyszerű a helyzet. Van, amikor 2 elem nem elég, hanem ennél több kell. A következő ábrán ugyanazt az alakzatot 4-4 egyforma pentominó elemmel raktuk ki:

Ez a legkedvezőbb megoldás. Tehát a P és az X elemekből nem elég 2 vagy 3, hogy egyforma alakzatot alkossunk.
A 12 különböző pentominóból kettőt kiválasztani 66 módon lehet. Minden kiválasztott párral ugyanaz a feladat, a lehető legkevesebb elem felhasználásával rakjunk ki egyforma alakzatokat. A párok nagy többsége (44 a 66-ból) 2 elemmel is megoldható. Érdekes, hogy az Y elem (bár nem szimmetrikus) ebben a feladattípusban a "legkezesebb", minden másik elemmel párba állítva elég 2-2 belőlük azonos formák kirakásához. Érdemes megpróbálkozni vele, azért nem olyan sima ügy, mint ahogy hangzik! A másik "egyszerű" elem a P, a fent látható X-en kívül minden más elemmel elég 2 darab az azonos alakzathoz.
Néha azonban jóval több elemre is szükség lehet:

A W és T pár 14 elemet igényel, ez a ma ismert legjobb megoldás.
Nekem furcsa, hogy az egyszerűnek tűnő Z és I pár 20 elemet igényel. Nagyon nehéz megtalálni a megfelelő alakzatot!
De nem ez a rekorder! A legtöbb szimmetriával rendelkező X elem különösen barátságtalanul viselkedik ebben a játékban. Az N-nel párba állítva 44 elemet igényelnek. Az összes pár közül ehhez szükséges a legtöbb elem a mai ismereteink szerint. És egyedül az X-hez tartoznak megoldhatatlan párok: belátható, hogy az X-szel és az I, U vagy V elemekkel nem lehetséges azonos alakzatokat kirakni. De az X még további érdekességet is tartogat: a W és a Z elemekkel nem tudjuk, hogy megoldható-e a feladvány. Íme az első megoldatlan probléma, lehet kísérletezni!
Az előző képen a W és a T felcserélhetőségére láttunk példát. Érdekes és szép, hogy a minimális alakzatban lyukak vannak. Ám azt is érdemes vizsgálni, hogy ha nem engedünk meg lyukakat, akkor is felcserélhetők? Létezik lyuk nélküli alakzat, ami mindkét elemmel kirakható? A válasz igenlő, és csak 2-2 elemmel szükséges több hozzá. Nagyon nehéz, de próbálja megtalálni az olvasó a megoldást!
Általában a lyuk nélküli problémák nehezebbek. Nagyon szép a W és Z pár 10 elemes alakzata (ez a szám 4 volt a lyukas esetben). Szintén 10 elem szükséges az I, V pár luk nélküli megoldásához.
Egy pici módosítással még bonyolultabbá tudjuk tenni ezt a feladványtípust. A ma ismert megoldások közül az összeshez páros számú elem szükséges, hogy a minimális kirakást megkapjuk. Adódik a kérdés, hogy mi a helyzet páratlan számú elemmel? Lehetséges egyáltalán 3-3 vagy 5-5 elem felhasználásával egyforma alakzatokat kirakni? Szerencsére igen. A második képen szereplő F és W elemekből 5-5 darabot használva kirakható azonos alakzat:

Ez elég megdöbbentő, nem? Hogy néz ki ez az alakzat? Hogy lehet egy ilyet megtalálni?
Egyszerűbb (3 darabos) az F, L és az F, P vagy az F, Y pár. Van még jópár 3 darabos megoldás, próbáljon néhányat megtalálni az olvasó! Érdemes a P elemmel próbálkozni! Aztán elég sok 5-7 elemes megoldás is létezik. De pl. az L, X pár 137 elemmel lesz csak felcserélhető, ez a ma ismert rekorder!
A hasonló típusú feladványoknál általában számítógépes segítséget is igénybe vesznek a játékosok. Azonban sokszor annyira nagy az esetszám, hogy a "nyers erő" nem elég, kivárhatatlan ideig futnának a programok. Ezért általában valami heurisztikát, ötletet tesznek az algoritmusokba a fejlesztők, csak jussanak eredményre! Az itt közölt nagyobb számok csak valószínűleg a legjobb megoldások. Aki érez magában kedvet és türelmet, nyugodtan álljon neki hasonló problémáknak, lehet javítani vagy megerősíteni a már ismert eredményeket.
De érdemes valahogy elkészíteni pár pentominó készletet is. Igazán jó móka rakosgatni az elemeket!