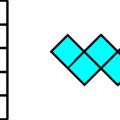
A hexominók hat négyzet összeillesztésével keletkeznek. Összesen 35 különböző létezik belőlük, a teljes készletről korábban már volt szó. A 35 elem túl sok egy jó játékhoz, annyira nehezek az összes elemet használó feladványok, hogy pusztán emberi erővel szinte lehetetlen megoldani azokat.
Vannak azonban érdekes részhalmazai a hexominó elemeknek. Teljesen logikusan adódott a kockahálókat alkotó csoport, viszont ez nem túl sok sikerélményt adott. Induljunk ki fordítva! Először határozzuk meg a kirakandó alakzatokat, és vizsgáljuk, hogy vannak-e olyan készletek, amikből minél több minden összeállítható.
Ha a hexominókat nem négyzetekből, hanem kockákból készítjük el, akkor térbeli alakzatok kirakására is alkalmas elemeket kapunk. Vizsgáljuk pl. a 8 elemből kirakható formákat. 8 hexominó összesen 48 kis kockából áll, ami sokféle geometriai idom összeállításával kecsegtet.
Nyolc elem nem olyan sok. Hogy ne legyen túl egyszerű a játék, keressünk olyan hexominó elemkészletet, amiből minél többféle alakzat kirakható, de az egyes alakzatoknak minél kevesebb megoldása legyen. Vajon vannak-e olyan elemek, amikből több szép forma is összeállítható, de mindegyik csak egyféle módon? A válasz pozitív, pl. az alábbi képen látható elemek ilyenek:

Ezekből az elemekből kirakható a 12×4-es téglalap:

Összeállítható belőlük a 8×6-os téglalap is:

És téglatestek is. Pl. a 6×4×2-es:

Vagy a 4×4×3-as:

Mind a négy fenti alakzat csak egyféleképpen rakható ki, így a kevés elem ellenére elég nehéz játékokat kapunk. (Amikor le akartam fotózni a fentieket, jó sokat elidőztem, az összerakással. Lehet, hogy egy nap alatt sem végeztem volna, ha nem veszek igénybe számítógépes segítséget :))
Vannak-e más, hasonló készletek? Nem túl sokan, de vannak. Pl. a következő elemek rendelkeznek ugyanezekkel a tulajdonságokkal:

És ezek is:

E készletek közül akármelyiket "kifaragva" egy jó nehéz és változatos játék birtokosai leszünk.
A fentieken kívül még érdekes próbálkozni más formák kirakásával is. A 48 nem négyzetszám, így négyzetet nem lehet összeállítani ezekből az elemekből. Viszont a 49 az már négyzetszám. Vajon, ha egy mezőt elhagyunk egy 7×7-es sakktáblából, akkor kaphatunk-e kirakható alakzatot? Az első elemkészlettel igen:

Itt pont a sarokmezőt hagyhattuk el. El lehet-e másikat is? És a másik készletek is alkalmasak ilyesmi majdnem-négyzetek kirakására? A válasz mindkét kérdésre igen. A pontos részletek vizsgálatát az olvasóra hagyom. (Jó nehéz feladat!)
Feltűnő, hogy az eddig bemutatott készletekben viszonylag sok a közös elem. Alaposan szemrevételezve megállapítható, hogy a fenti 3 készlet mindössze 11-féle elemből áll. Ezekből:

Tehát, ha valaki elkészíti ezt a 11 elemet, máris lesz három jó nehéz játéka. De tényleg csak három? Nincs több lehetőség ebben a készletben? Dehogynem!
A 11 elemből 8-at 165-féle módon lehet kiválasztani, vagyis a fenti elemekből 165 különböző 8 elemű készletet hozhatunk létre. Ezek nem mindegyike igazán érdekes, sőt van olyan, amivel az eddig ismertetett alakzatok közül egyik sem rakható ki.
Hogy más érdekes készletekről is tudjak írni, betűzzük meg az előbbi képen látható elemeket!

(Az elsőnek bemutatott készlet az ABDFGHIK, a második az ABCDFGIJ és a harmadik az ABCEFHIJ elemekből áll.)
Létezik még egy igazi térbeli téglatest, ami 48 kockából áll és eddig nem szerepelt, ez pedig a 8×3×2-es. Az eddig ismertetett készletekből nem lehet kirakni. De a 11 elemből kiválasztható 8 úgy, hogy összerakható legyen. Talán meglepő, de egyetlenegy ilyen elemnyolcas létezik, ez pedig az ABCDFGHI. Íme az eddig hiányzó téglatest:

Ebből a készletből még a 8×6-os téglalap és a 6×4×2-es téglatest is összeállítható.
Térjünk vissza egy pillanatra a 7×7-es négyzetből elhagyható mezőhöz! Azt az egy mezőt 10 helyről hagyhatjuk el, a többi lehetőség mind előállítható ezekből forgatással. Ez a 10 lehetőség:
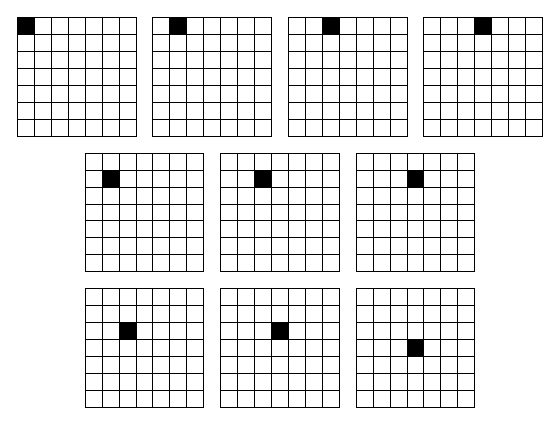
Az elsőre már láttunk kirakott példát. Az utolsó, amikor középen van a kihagyott mező, sajnos nem rakható ki az először bemutatott készlettel, de a másik kettővel igen, méghozzá ezeknek is csak 1 megoldása van. Így az a két készlet nem is csak négyszeresen egyedi, hanem legalább ötszörösen!
A hiányos sakktáblákkal és a téglatestekkel együtt 15-féle alakzatról volt eddig szó. A 3-diknak bemutatott készlettel a 15-ből 10 alakzat kirakható, ezzel rekorder. De csak holtversenyben, mert az ACDFGHJK elemekből is pontosan 10 rakható ki, bár összesen sokkal több megoldásuk van, mint az eredeti készleteknek.
Érdekes szélsőség még a BCDEFIJK készlet. Ebből csak egyetlen téglatestet lehet kirakni, azt is egyféleképpen. A sakktáblák közül az egyiket sem.
Három téglatest állítható össze az ACDEFHJK készletből és ezeken kívül még 6 sakktábla. Ezzel szintén előkelő helyen szerepel a változatos készletek sorában.
Készítettem magamnak egy nagy táblázatot, ami összefoglalja a 11 elemből kirakható alakzatokat. A táblázatban 700-nál több lehetőség szerepel, vagyis mondhatjuk, hogy ezzel a 11 elemmel minimum ennyi feladvány oldható meg. Vajon mennyi idő lenne azt mind kézzel-fejjel végigjátszani?
(Kísérletezem a fotózással, remélem tetszenek az új képek. Nem mondom, hogy mindig ilyen lesz, de próbálkozom szép képek készítésével. Ha zavaró, vagy a megértés rovására megy, szóljatok!)