Nagy örömömre ismét vendégposzt következik. Szilassi Lajos tanár úr, aki az általa felfedezett poliéderről lett világhírű egy remek játékot általánosított és alkotott belőle sok, különböző nehézségű feladványt.
Kör labirintussal – ezzel a címmel szerepelt a 2012. évi bakonysárkányi ördöglakat találkozón bemutatott puzzle-készlet abban a feladatsorban, amelyet a bakonysárkányi gyerekek, és e sorok írójához hasonló gondolkodású megszállott barátok kollégák zsűriztek.
Azt hiszem minden pályázó kollégám nevében mondhatom, hogy itt nem a győzelem, hanem a részvétel volt a fontos. Az, hogy megismerkedjünk izgalmasabbnál izgalmasabb új kézbe vehető feladványokkal, ördöglakatokkal, puzzle készletekkel.
Az itt bemutatott játéknak van egy kis előtörténete.
A Gathering for Gardner konferenciát kétévenként rendezik Martin Gardner tiszteletére, aki több mint 30 évig volt a Scientific American c. folyóirat matematikai rovatának a vezetője. E konferencia (átlagosan mintegy 200) részvevője magával szokott vinni elegendő példányszámban egy-egy apró tárgyat, „szellemi csemegét” amelyet minden résztvevő megkap. A 8-as számhoz kötődő (nyolcadik) G4G8 konferencia egyik ilyen feladata adta az ötletet e pályázat anyagához:
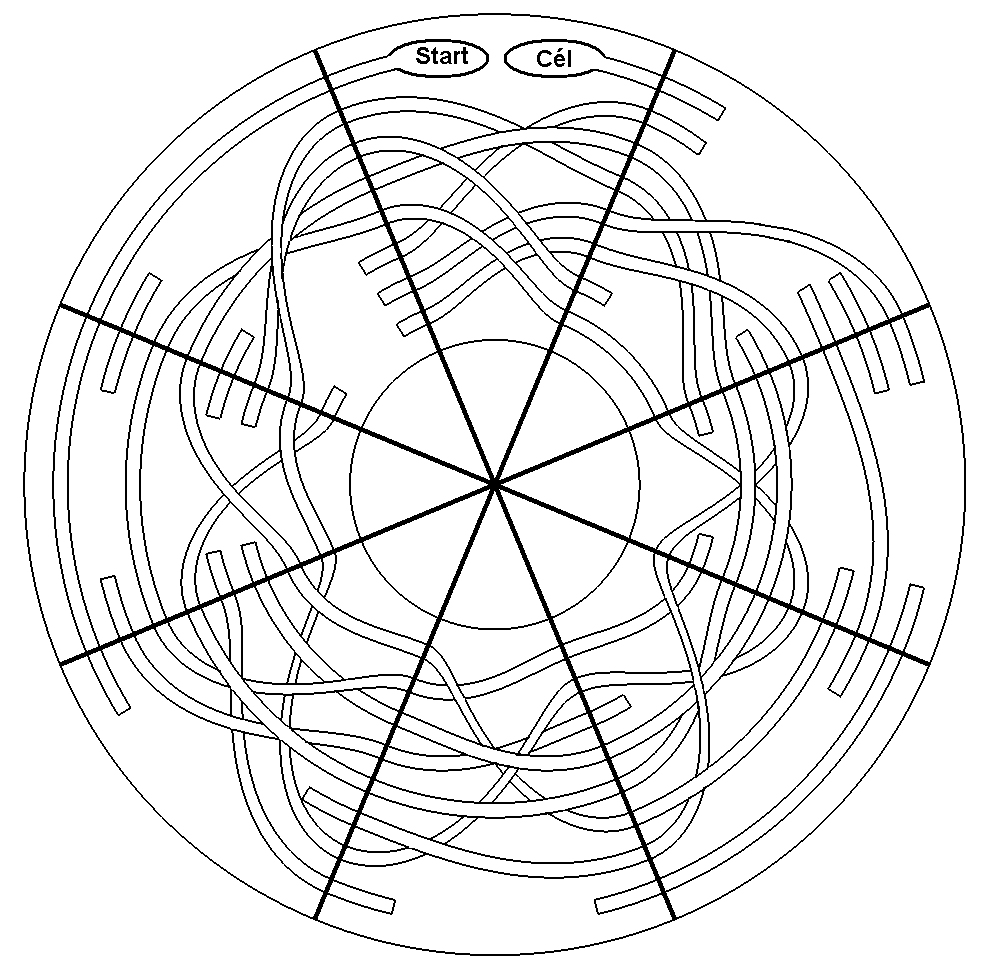
Vágjuk szét a körcikkeket, majd rakjuk össze úgy, hogy a „Start”-tól folytonos (egymás alatt futó) vonallal eljuthassunk a „Cél”-ig.
A feladat (számomra) túlságosan nehéznek bizonyult, 7!= 5040 lehetséges elrendezés közül kellene kiválasztani a megoldást. A megvizsgálandó esetek számát következetes próbálgatással alaposan le lehet szűkíteni, de ehhez nem volt elegendő türelmem.
Ahhoz viszont igen, hogy a feladat ötletét felhasználva készítsek egy számítógépi programot. Olyat, amely előállít tetszőlegesen sok ilyen jellegű könnyebb-nehezebb feladatot. Ha ezeket gyerekeknek szánjuk – hadd jöjjenek rá önállóan a szisztematikus keresés módszerére ‑ , akkor kapóra jött, hogy most, a hatodik bakonysárkányi ördöglakat találkozóra olyan feladatokat kellett (illett) vinni, amelynek köze van a 6-os számhoz. Ennek a tortának legyen csak hat szelete, akkor már nem is lehet több megvizsgálandó esetünk, mint 5!=720.
Ezzel előállt egy olyan „keverjük össze –bogozzuk ki” jellegű feladvány család, amelynek lehetnek egészen könnyű, kissé nehezebb és egészen nehéz változatai.
Anélkül, hogy untatnánk olvasóinkat a technikai részletekkel, bemutatunk egy könnyebb feladatot, és azt, hogy miként lehet matematikailag precízen leírni egy ilyen konstrukciót.
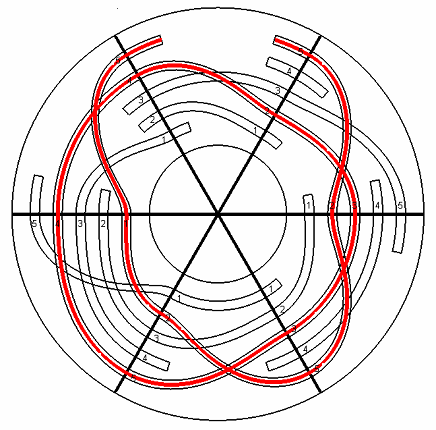
Itt egy olyan feladatnak az egyik lehetséges megoldását látjuk, amely 6 körcikkből áll, melyek mindegyike 5 helyen csatlakozik a mellette lévőkhöz.
Ennek a labirintusnak a leírására egy mátrixot (téglalapban elrendezett számokat) alkalmaztunk, mivel ezt a számítógép is könnyen „megérti”:.
A:= [[ 2, 4, 3,-1,-5],
[ 3,-5,-2, 4, 1],
[ 2, 3, 4, 5, 1],
[ 1, 5, 2,-4, 3],
[-5, 1, 3, 4, 2],
[-4, 5, 2,-1, 3]]:
A mátrix egy-egy sora egy-egy körcikket jelent. Az egy soron belül lévő számok pedig rendre azt mutatják, hogy a (belülről kifelé számozott) jobboldali csatlakozási helyektől rendre melyik baloldalihoz vezet az út.
Ha egy szám negatív, az azt jelenti hogy megszakítottuk a csatlakozást. Pl. a felsőtől balra eső körcikket, a 2. sor helyett így is leírhattuk volna: [ 3,-2,-5, 4, 1], hiszen a nem csatlakozó végpontok sorrendje bármi lehet.
Gondoljuk végig, hogy ha a mátrixban csak az első sor utolsó eleme lenne negatív, azaz csak a start-cél megszakítás lenne a rajzon, akkor a körcikkek bármelyik sorrendje megoldást adna.
Ha megoldást adó útvonalat leíró számokat kivéve minden egyéb szám negatív lenne, vagyis ahol csak lehet, megszakítást tennénk a rajzba, akkor pedig viszonylag könnyen meg lehetne találni a (nem feltétlenül egyetlen) megoldást, hiszen nem lenne olyan vonal, amely zsákutcába vezetne bennünket. Ha minden körcikk legkülső jobb és baloldali csatlakozási pontja össze lenne kötve, akkor is minden elrendezés megoldást adna, függetlenül a megszakítások számától és helyétől.
A feladatok nehézsége egyrészt attól függ, hogy hány körcikkre osztottuk a kört, a körcikkek hány helyen csatlakozhatnak, hány megszakítás van a körcikkeken és hány megoldása van a feladatnak. Ha pl. csak egy, és az is olyan, hogy a megoldást adó út a starttól a célig többször is körbe fut, akkor a feladat annál nehezebb, minél kevesebb megszakításunk van.
Például a 8 körcikkből álló feladatok közül a t8e8-a jelű 19 megszakítást tartalmaz, és 72 megoldása van, a t8e8-b -ben 32 megszakítással sikerült elérni, hogy csak egy megoldása legyen a feladatnak, ugyanakkor az Atlantából származó t8e8-x konstrukcióban a feladat szerzője mindössze 16 (!!) megszakítás mellett érte el, hogy ugyancsak egyetlen jó megoldás van. (Végül is ezt az erre írt „kibogozó” programmal derítettem ki.) Úgy látszik tud valamit a feladat szerzője, amit én ‑ egyelőre ‑ nem.
Mivel minden bizonnyal sokan keresnek egyszerűen elkészíthető játékokat, feladványokat, az alábbi feladatokat ilyen önállóan elkészítendő feladatoknak szánjuk. Elegendő a mellékelt (egyszínű, png formátumú) rajzokat – ha lehet vastagabb papírra ‑ kinyomtatni, szétvágni, esetleg furnérlapra ragasztani, és már készen is van egy jó kis „összekeverem-kibogozom” játék. A png fájllal azonos nevű txt fájl a feladat megoldását adó mátrix, így ha „szabad a gazda”, akkor is szükség van egy kis odafigyelésre a megoldás megkereséséhez.
Jó játékot kíván a feladványokhoz:
Szilassi Lajos
szilassi@jgypk.u-szeged.hu
| A feladat | A megoldás | Megoldások száma |
| t5e6-a.png | t5e6-a.txt | 10 |
| t5e6-b.png | t5e6-b.txt | 1 |
| t6e5-a.png | t6e5-a.txt | 6 |
| t6e5-b.png | t6e5-b.txt | 4 |
| t6e5-c.png | t6e5-c.txt | 57 |
| t6e5-d.png | t6e5-d.txt | 68 |
| t6e5-e.png | t6e5-e.txt | 4 |
| t6e6-a.png | t6e6-a.txt | 9 |
| t6e6-b.png | t6e6-b.txt | 6 |
| t6e6-c.png | t6e6-c.txt | 2 |
| t6e7-a.png | t6e7-a.txt | 2 |
| t6e7-b.png | t6e7-b.txt | 6 |
| t7e5-a.png | t7e5-a.txt | 32 |
| t7e6-a.png | t7e6-a.txt | 62 |
| t7e6-b.png | t7e6-b.txt | 6 |
| t7e6-c.png | t7e6-c.txt | 1 |
| t8e7-a.png | t8e7-a.txt | 1 |
| t8e8-a.png | t8e8-a.txt | 72 |
| t8e8-b.png | t8e8-b.txt | 1 |
| t8e8-x.png | t8e8-x.txt | 1 |
| Új feladványok | ||
| t7e5-b.png | t7e5-b.txt | 4 |
| t8e5-a.png | t8e5-a.txt | 2 |
| t8e6-a.png | t8e6-a.txt | 2 |
| t8e7-b.png | t8e7-b.txt | 1 |