A "kissé" szenzációhajhász cím talán indokolt, ha ha figyelembe vesszük az előzményeket. A Félkész őrület nevű játékról szóló bejegyzés elég népszerű volt. Jópáran elkészítették a színes kockákat és több kérdés is felmerült. Meg izgatott a probléma, hogy vajon csak a véletlen, hogy létezik ilyen kockakészlet? Egyáltalán van másik hasonló? Több vagy kevesebb kockából, színből is lehet hasonlót alkotni?
Belekezdtem egy nagyobb számítógépes vizsgálatba és bizony jutottam néhány érdekes eredményre. Ezekről szól ez a bejegyzés.
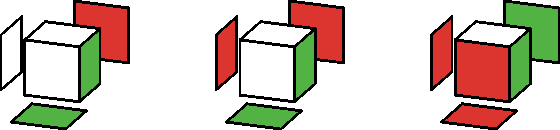
Először nézzük a már bemutatott négy kockából és négy színből álló változatot! Adott tehát 4 kocka, az oldalaik 4 színnel vannak színezve. Minden kocka különböző. A feladat szerint egy tornyot kell készíteni belőlük úgy, hogy a torony minden oldalán csupa különböző színű oldal látszódjon:

A fotón csak 2 hosszú oldal látszik, azokon tényleg különbözőek a színek. (Elárulom, hogy ebben az elrendezésben a két nem látszó oldalon nem így van, nem akartam lelőni a megoldást.)
Az első megválaszolandó kérdés az volt, hogy egyáltalán hány 4 színnel színezett különböző kocka létezik. Fontos, hogy mind a négy szín szerepeljen minden kockán. Nem is olyan egyszerű megszámolni, gyakori hiba, hogy forgatással egymásba vihetőket különbözőknek hiszünk. Biztos "kézzel" is meg lehet számolni az eseteket, de én az ilyesmit mindig el szoktam rontani. Egy program is tud hibázni, de azért azt le lehet ellenőrizni. Ezt a kérdést viszonylag hamar sikerült megválaszolni: 68-féle 4 színű kocka létezik. Meglepően sok, én ennél kevesebbre tippeltem volna.
A 68 kockából 4-et kell kiválasztani ehhez a játékhoz. Ezt több mint 800 ezer módon lehet megtenni. Itt már sejtettem, hogy sokat fog a számítógép dolgozni :) Viszonylag hamar elkészültem azzal a programrésszel is, ami leellenőrizte, hogy 4 kockából lehet-e "jó" tornyot képezni. Egy kockát 24-féle módon forgathatunk. (6 lap lehet a tetején és ehhez lehet 4 szemközti lapot választani.) A 4 kocka elvben 244=331776 módon állhat. Ezt a nagy számot egy kicsit csökkenthetjük a vizsgálat során, hisz pl. a legalsó kockánál csak az számít, hogy melyik oldalpár van alul és felül, így az alsó kocka csak 3 helyzetben lehet. De még így is 41472 állást kellet ellenőrizni 4 kockánként. Minden állást megvizsgáltam, mert kíváncsi voltam arra is, hogy egy-egy kockanégyesnek hány megoldása van, ha van egyáltalán.
1-2 nap alatt lefutott a program, és ekkor jött az első meglepetés. A több mint 800 ezer lehetőségnek több mint fele alkalmas jó torony készítésére. Tehát volt közel 490 ezer kockakészletem, ami alkalmas erre a játékra :) Mi legyen a következő lépés? Adódott, hogy csak a kevés megoldásos készleteket vizsgáljam tovább. De van-e még olyan készlet, aminek nagyon kevés, esetleg csak 1, 2 megoldása létezik? A válasz pozitív, méghozzá nem is olyan ritkák az 1 megoldásos készletek, több mint 25 ezer van belőlük! Ez már igen, így van 25000 félkész őrületem :)
Vajon nem lehet-e még egy csavart adni a játéknak? Nincs-e néhány készlet, amivel más játékot is lehet játszani, esetleg sokkal könnyebbet?
Elhatároztam, hogy azt is megvizsgálom, hogy a 4 kockát nem lehet-e elrendezni egy 2*2-es négyzetbe, úgy hogy annak az oldalai meg azonos színűek legyenek:

Amint a képen is látható, voltak ilyen kockakészletek, de ebből már jóval kevesebb. Összesen 340 olyan kockanégyes létezik, amiből 1 megoldásos torony rakható ki és a négyzetnek is csak 1 megoldása van. Ezek jó nehéz játékok! (Később megtaláltam, hogy más is felfedezte pontosan ezt a játékot, árulták is Mutando néven. A színezése más volt, és nem tudom, hogy egy megoldásosak voltak-e az ő feladványaik.)
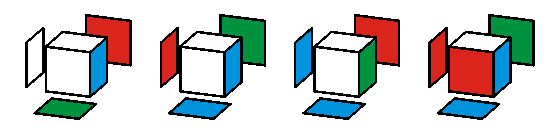
Egy ilyen készlet fotói láthatók a fenti képeken. Hogy mindenki elkészíthesse a saját változatát, következzen most rajzban is, ahol a hátsó oldalak színe is kivehető:
Ez volt a cserejátékom a 6. Ördöglakat találkozón Bakonysárkányban. Ezeken a találkozókon verseny is van, ahol a játéknak kapcsolódni kell az éppen aktuális sorszámhoz. Így elhatároztam, hogy megvizsgálom ezt a játékot 6 kockára, 6 színnel.
Mindössze 30 különböző 6 színű kocka létezik. Ez talán meglepő a 68 db 4 színűhöz viszonyítva. A 30-ból 6-ot kiválasztani közel 600 ezer módon lehet. A 6 kockának viszont rengeteg állása van: 3*245 ami közel 24 millió. Így nem volt reális az összes lehetőség elemzése. Helyette véletlenszerűen választott a program 6 kockát és azokat vizsgálta. Mindezt rengetegszer megismételve. Így nem szolgálhatok teljes eredménnyel, de jópár olyan készletet találtam így is, aminek csak egy megoldása van. Íme az egyik:

De nem álltam meg itt, a 4 kockás eredményeken felbuzdulva itt is kerestem más elrendezést. A 6 kocka 2*3*1-es téglatestbe rendezhető. Azokat a készleteket kerestem, ahol ennek a téglatestnek minden oldalán csupa különböző színek láthatók:



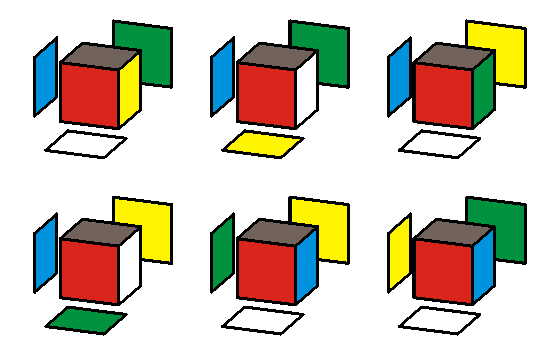

A fotón is látszik, hogy ez nem a jó elrendezés. A kockák teteje különböző, bal alulról nézve is, de jobbról már látszik két zöld lap.