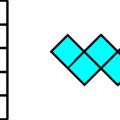
A tangram a kirakós logikai játékok egyik legismertebb csoportja. Nagyon sokféle hasonló játék létezik a tojás alakú tangramtól a szív alakúig. Az V. Országos Ördöglakat Találkozóra az ötös szám jegyében Gáspár Merse Előd egy olyan tangram változatot készített, amelynek minden tagja ötszög. Az alkotó koncepciója az volt, hogy csak rácsötszögek szerepeljenek a készletben, azaz olyan ötszögek, amelyeknek a csúcsai egy négyzetrács csúcsaira esnek, továbbá az, hogy legfeljebb két különböző oldalhosszúság szerepeljen. Rácsegységekben mérve a használt oldalhosszak nem mások lettek, mint kettő és gyök öt. Ez utóbbi az egy és kettő hosszúságú szárakkal rendelkező derékszögű rácsháromszög átlójának hossza. Ezen két oldalhosszúság közti relatív különbség csupán 12% körüli, ami odafigyelést igényel a játék során, ezért segítséget jelenthet, ha az ötszögek éleit hosszuk alapján két színnel színezzük. A fenti feltételeknek összesen tíz különböző rácsötszög felel meg. Így összesen 5+5 elem szerepel a pentangramra keresztelt játékban, természetesen mindez az ötös szám jegyében. A kirakó érdekessége, hogy az elemek között szerepelnek konkáv alakzatok is, és a pentominó és más kirakós játékokhoz képest szakít a derékszögekkel. A pentangram további érdekessége, hogy a hagyományos tangramokhoz képest inverz módon jött létre, azaz nem egy meglévő alakzatot vagdosott részekre az alkotó, hanem adott tulajdonságoknak eleget tevő összes ötszög alakú elemet vette számba.

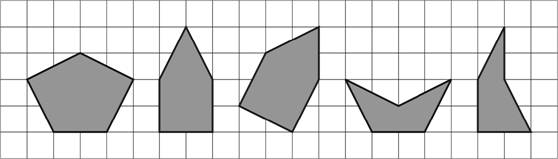
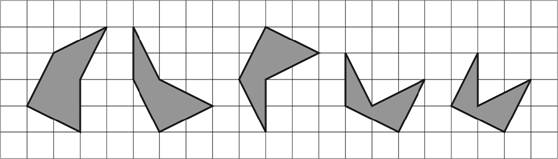
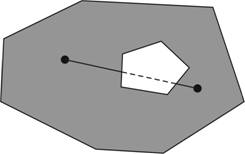
A pentangram alap feladata, hogy az összes elem felhasználásával készítsünk egy konvex alakzatot. A játék során a kirakó elemei természetesen megfordíthatók, így minden elemnek a tükörképe is egy lehetséges elhelyezési mód. A konvex tulajdonság azt jelenti, hogy a síkidom bármely két pontját összekötő szakasznak minden pontja is a síkidom része. A fenti alapelemek közül például csak az első három konvex, a többi konkáv, melyekben homorúszög is található. Mivel konvex alakzatot kell kiraknunk, az alakzatnak feltétlenül összefüggőnek kell lennie, azaz minden elemnek érintkeznie kell a korábbiakhoz, nem lehet az alábbi példához hasonló, mert az sértené a konvexitási tulajdonságot.

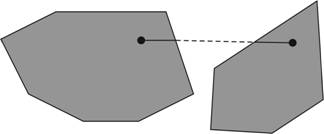
Nem lehet továbbá az alakzatban lyuk, illetve nem lehet a kerülete mentén homorúszög, mert ezekben az esetekben is sérülne a konvexitás, lásd az alábbi ábrákat.

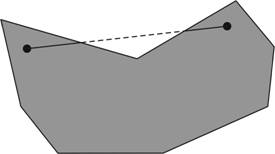
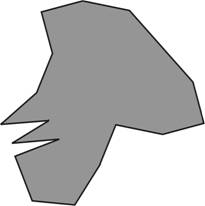
Természetesen a tangramhoz hasonlóan itt is rengetegféle alakzatot ki lehet rakni, mint például az alábbi török emberfejet turbánnal. De mivel az alkotóelemek között sok a konkáv, ezért a kirakott alakzatok nagyrésze is konkáv lesz. Ezért is érdekes az alap feladat, miszerint rakjunk ki egy konvex alakzatot az összes elem felhasználásával. További érdekesség, hogy a megoldásban újra felbukkan az ötös szám, de hogy miként, az maradjon titok egyelőre. Aki a megoldást elsőként tölti fel, az ajándékba kap egy könyvet.

Gáspár Merse Előd © 2011