Mindig örülök, ha látom, hogy sikerül felkelteni mások érdeklődését egy-egy játék iránt. Az azonban meglepett, hogy talán a blog történetének legalaposabb elemzését egy vendégszerző végzi el. Lehet, hogy részletesebben, körültekintőbben járt el, mint az eredeti játék megalkotói! Legalábbis a cikk vége felé található következtetések ezt látszanak igazolni!
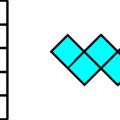
Az "Azonosság - L" című postból megismert játék meglehetősen egyszerűnek tűnik: könnyen elkészíthető, és a játék szabályai is könnyen érthetőek. Ugyanakkor Péter leírása alapján a megoldása nem egyszerű, sőt kifejezetten nehéz. Ez számomra egyből vonzóvá tette, és gondoltam kipróbálom magam rajta, mert a cikket olvasva ötletem is volt, hogyan kezdenék hozzá. Papírból vágtam ki a két játékot, és nekiálltam a próbálgatásnak.
A zöld-lila játékhoz találtam egy megoldást, ami később "hibásnak" bizonyult, mert a feladat leírása alapján a folytonosság kritériuma nem volt akkor egyértelmű számomra. A piros-fekete játéknak az ötletem alapján az egyik megoldását megtaláltam viszonylag hamar. Miután Péterrel tisztáztuk a folytonosság kritériumát, pár órás próbálkozás után (tényleg nehéz a játék) a piros-fekete második megoldása is meglett. A zöld-lila helyes megoldását viszont hosszas próbálkozás után sem találtam. Végül feladtam, és szoftveres elemzéssel 20 másodperc alatt meglett az eredmény. Péter javaslatára - és mivel akkor már engem is érdekelt a dolog mélyebben - nekiláttam, hogy szoftver segítségével feltérképezzem ezt a játékot.
Hány darab megoldással rendelkező készlet létezhet? Vannak könnyű és nehéz készletek? Az IPP-n bemutatott két készletben van valami különleges? Milyen lehetőségeket rejt még ez a játék?
Ezekre a kérdésekre igyekszem most választ adni.
Azonosság L játék:
Először is a feladat:
Két színnel csempézett két-két darab pento- és tetrominot kell úgy elhelyezni, hogy a létrejövő alakzatban mindkét szín összefüggő (a csempék élen illeszkednek) alakzatot alkosson, és a két szín alkotta alakzatok forgatással és tükrözéssel egymásba transzformálható legyen.
Íme egy példa, ahol a fehér és a piros csempék alkotta alakzatok "azonosak":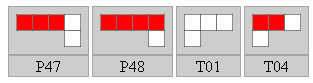
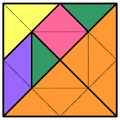
és a megoldása:
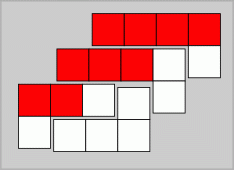
Könnyen belátható, hogy a megoldásnak szükséges - de nem elegendő! - feltétele, hogy a két pentomino (későbbiekben P) és a két tetromino (későbbiekben T) csempéi közül 9 db az egyik, míg 9 db a másik színnel legyen színezve. Illetve azt is könnyű belátni, hogy amennyiben egy készletnek van megoldása, úgy a készlet minden elemét tükrözve szintén (az előzővel ekvivalens) megoldással rendelkező készletet kapunk. Valamint ha a színek "inverzeit" vesszük minden elemen, akkor is az eredetivel ekvivalens megoldásokkal rendelkező készletet kapunk.
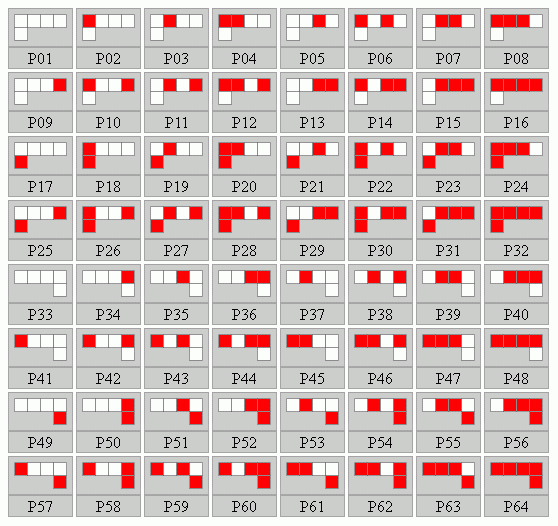
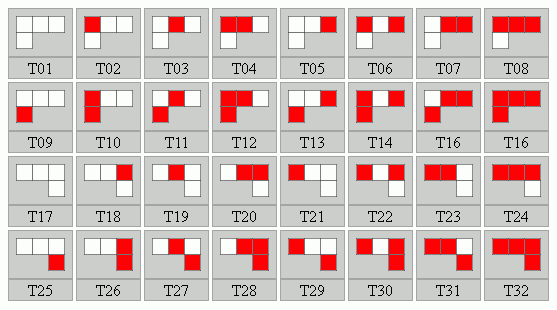
Egy P elem 32, míg egy T elem 16-féle módon színezhető két színnel. De az L-ek tükörképe ebben a játékban külön elemnek számít, ezért lényegében 64 db P és 32 db T létezik. Ezek a következőek:
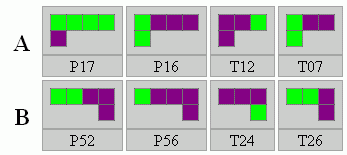
Az IPP-n feltűnt játékok kétoldalasak (A és B oldal), így egyes L-eket megfordítva újabb készleteket nyerünk. A két eredeti kétoldalas játék:
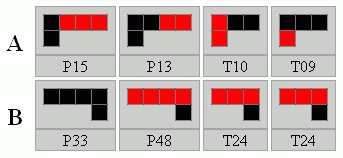
A piros-fekete játékban, csak két olyan készlet érhető el, ahol a két szín 9-9 arányban szerepel, így a forgatásokkal előállítható 16 db készlet közül csak 2 játszható: P16, P13, T24, T09, illetve P33, P48, T10, T24. Ennek a kettőnek egyébként van is megoldása.
A zöld-lila játékban három játszható készlet is létrehozható, de csak az egyiknek van megoldása: mindig P17, P16 a két P, míg a T elemek bármelyik párosítása megfelelő (de a T07/T26 szimmetriája miatt csak 3 fajta T pár létezik). Részben ez adja a játék nehézségét, mivel meg kell találni először a helyes készletet, utána pedig még a készlet megoldását is. Én több óra után sem jártam sikerrel, és egy idő után úgy éreztem körbe-körbe járok ugyanazon próbálkozások mentén.
Először tekintsünk el a kétoldalas játékoktól, hiszen ezek csak a játszható készletek számosságát bővítik, de valójában a cél egy konkrét készlet megoldása. A készletet a későbbiekben 2P2T-vel is fogom jelölni, amely azt fejezi ki, hogy 2 db P és 2 db T elemből áll.
A fenti színezés számosság mellett 4.194.304 darab 2P2T készlet alakítható ki összesen, ezekből azonban csak 44.008 olyan, hogy az elemek színezése kiegyensúlyozott, így van elméleti lehetőség a megoldásukra (játszhatóak). Azonban mindössze 1.842 esetben van megoldás: 856 esetben 1 db megoldás van csak, míg vannak többezer megoldással rendelkező készletek is. Ez azért elég szép számú játékot jelent.
Ezek a számok egyébként a készletek tükörképeit és az inverz színezett készleteket is tartalmazzák.
Vannak olyan P színezések, amelyekre nem létezik megoldható készlet, és olyanok is, amelyekre csak viszonylag kevés készlet rendelkezik megoldással. Ezek jól sejthetően a pepita elemek:
- P10 ( és inverze P23, és tükörképeik P42 és P55 ) esetén nem alakítható ki megoldással rendelkező készlet
- P06 ( és inverze P27, és tükörképeik P38 és P59 ) esetén csak két készletnek van megoldása: P06, P27, T01, T16 és P06, P27, T17, T32. Ezek egyébként egymás inverz tükrözöttei.
- P14 ( és inverze P19, és tükörképeik P46 és P51 ) esetén csak hat készletnek van megoldása
- P12 ( és inverze P21, és tükörképeik P44 és P53 ) esetén csak hat készletnek van megoldása
A T elemek esetén is vannak olyanok, amelyek ritkán vesznek részt megoldható készletben, de ott minden elemhez létezik készlet.
Nagyon sok megoldással pedig általában azok a készletek rendelkeznek, ahol a két P és/vagy a két T elem egyszínű, vagy egymás tükörképe, esetleg inverz színezettje. Például a P01, P32, T01, T16 készlet 6.608 megoldással rendelkezik.
Ha ezekből a feltételekből elveszünk, akkor egyre szűkül a megoldások száma, míg ha egyik sem teljesül (egyszínűség, tükrösség, inverz színezettség) akkor általában 1 vagy 0 megoldás van már csak.
Az IPP-s készletek esetén is igaz, hogy a fenti kritériumok nem teljesülnek, nem meglepő tehát, hogy csak egy megoldásuk van. Azonban rengeteg hasonló készlet létezik még, így ez a kettő játék semmi kitüntetett jelentőséggel nem bír. Ha pedig figyelembe vesszük azt, hogy a játékoknak két oldala van és akár több készlet is kialakítható belőlük, akkor sokkal nehezebb, illetve akár könnyebb/sokszínűbb játék is található.
Két példa, mindkettő hasonló nehézségű mint az IPP készletek:
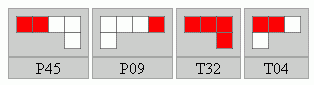
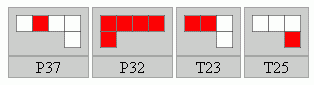
Kétoldalas készletek:
Kétoldalas készletek esetén a könnyedséget vagy a nehézséget éppen az adja, hogy az elemkészlet egy-egy oldalán található készletek variálhatóak egymással egyes (vagy akár az összes) elemet megfordítva, így a forgatásokkal 16 darab készlet alakítható ki. Azonban könnyen lehet, hogy ezek közül csak némelyik játszható, mert a két szín egyensúlyát bizonyos kombinációk megbontják.
Mind a 16 db készlet csak akkor játszható, ha minden elem olyan, hogy a két szín aránya minkét oldalukon azonos, hiszen így megfordítva őket a színek továbbra is egyensúlyban maradnak.
Egy kétoldalas készletnek csak akkor van értelme, ha legalább két darab játszható készlet kialakítható belőle; de hogy egynél több készletnek van-e megoldása az már más kérdés.
Elsősorban olyan készletpárokat vizsgáltam, amelyeknél igaz, hogy minden elemnek ugyanolyan arányú színkiosztás szerepel mindkét oldalán, és így mind a 16 db készlet játszhatóvá válik. Hogy a 16 darabból hánynak van megoldása, azt itt is elsősorban azok a szempontok befolyásolják, mint a sima egyedülálló készleteknél: elem egyszínűsége, P-k és/vagy T-k tükrössége, inverz színezettsége. Plusz a megoldható készletek számát jelentősen növeli ha bizonyos elemeknek az A oldala a B oldal tükörképe.
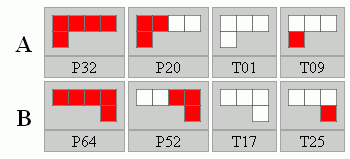
Például a P32, P20, T01, T09 és P64, P52, T17, T25 készletpárból kialakítható kétoldalas játék mind a 16 készlete rendelkezik 1-6 db megoldással (nyilván erősen szimmetrikus, ismétlődő alakzatok vannak közöttük). Itt az A oldal mindig a B tükörképe, és van benne két egyszínű elem is.
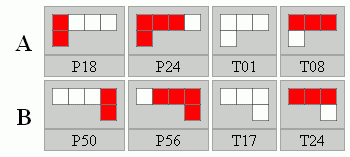
Csökkentve a feltételeket, és egyetlen egyszínű elemet megengedve kapjuk például a következő készletpárt: P18, P24, T01, T08, és P50, P56, T17, T24. Itt 12 készlet rendelkezik megoldással, mindegyik 1-1 darabbal. Az A-B tükrösség miatt ez lényegében 6 megoldás, és a szimmetria párjaik.
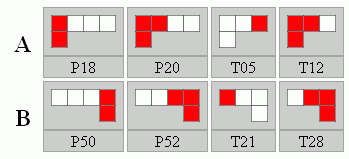
Ha az A-B tükrösséget megtartjuk, de egyszínű elemet nem engedünk, akkor már kicsit nehezebb játékot kapunk, például: P18, P20, T05, T12 és P50, P52, T21, T28. Itt már csak 6 készlet rendelkezik 1-1 megoldással, de az A-B tükrösség miatt valójában ez csak 3 megoldás, és a szimmetria párjaik.
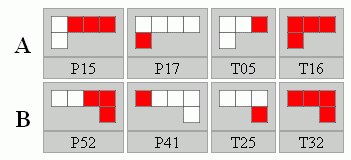
Ha az A-B tükrösséget elvesszük, akkor is találhatóak még több megoldható készletes játékok, például: P15, P17, T05, T16 és P52, P41, T25, T32. Itt 8 készlet rendelkezik 1-1 megoldással.
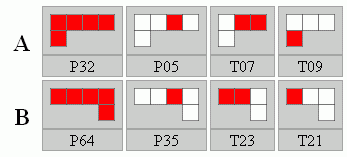
Az igazán nehezek azok a játékok, ahol mind a 16 készlet játszható, de csak egynek van megoldása, és annak is csak 1 db. Erre példa az alábbi játék: P32, P05, T07, T09 és P64, P35, T23, T21.
Változó elemszámú készletek:
Felmerül a kérdés, hogy ha adott egy 2 db P és 2 db T által alkotott készlet, akkor lehet-e ezt bővíteni, csökkenteni úgy, hogy szintén játszható maradjon.
A bővítést egyelőre még nem vizsgáltam, de ha lehet is, akkor nyilván csak páros számú csempét tartalmazó elemekkel, így 1 db T, vagy 2 db P hozzáadásával. Amennyiben 1 db T-vel kell bővíteni/csökkenteni a készletet, akkor annak a színezése 2-2 arányban kell, hogy legyen.
A csökkentést vizsgáltam meg, vagyis, hogy 2P1T és 2P játékok léteznek-e, illetve létezik-e olyan 2P2T készlet, ami bármelyik (akár mindkettő) T elem elvételével is megoldható marad.
A 2P játék (csak két pentomino) esetén 504 játszható készlet alakítható ki, de csak 16 darabnak van megoldása. Ezek szinte mind inverz színezett P elemekből állnak. Egyetlen kivétel a P13, P15 pár, és ennek inverz színezett, és tükrös párjai.
A 2P1T játékból 13.888 játszható készletből 204 darabnak van megoldása. Itt is vannak kevés megoldással rendelkező, nem feltétlenül szimmetriára építő készletek, például: P33, P24, T24.
Ha azonban olyan 2P2T megoldható készletet keresünk, ahonnan szabadon elhagyható bármelyik T elem és a kapott 2P1T játékok is megoldhatóak, akkor igazából már csak szimmetriára építő készletek jöhetnek szóba. Ilyen készlet például a P15, P18, T23, T26. Itt mind a 2P, mind a kettő 2P1T, és a 2P2T is megoldható, utóbbi meglehetősen sok megoldással rendelkezik.
Az előbbi készletet egy másikkal kétoldalassá bővítve olyan játékot kapunk, amelyből több megoldható készlet is kialakítható elemek elvételével: P15, P18, T07, T10 és P52, P45, T23, T26
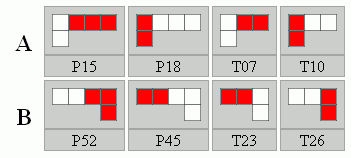
Itt megoldhatóak (sokszor többféleképpen is):
- P15, P18
- P52, P45
- P15, P18, T23
- P15, P18, T26
- P52, P45, T23
- P52, P45, T26
- P15, P45, T10
- P52, P18, T07
- P15, P18, T23, T26
- P52, P45, T07, T10
Az alábbi készletből is több 1 vagy 2 megoldással rendelkező 2P2T és 2P1T készlet alakítható ki: P01, P24, T07, T12 és P33, P48, T23, T24
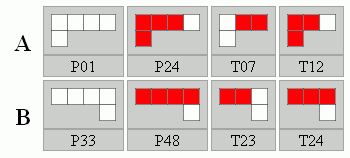
Itt a megoldható készletek:
- P33, P48, T24
- P33, P48, T12
- P33, P24, T24
- P33, P24, T12
- P01, P48, T24
- P01, P48, T12
- P01, P24, T24
- P33, P48, T24, T07
- P33, P48, T12, T23
- P01, P48, T24, T23
- P01, P48, T24, T07
- P01, P48, T12, T07
- P01, P24, T24, T07
Az elemző szoftverről:
Az eredeti IPP-s játékok megoldásához használt program "erőből" próbálta megoldani a feladatot. Egy fix méretű játéktér közepén a készlet egyik pentominoját fix állásban elhelyezte, és a többi három elem különböző permutációit különböző elforgatások (0/90/180/270) mellett próbálta hozzáilleszteni, majd ha sikerrel lerakta mindegyik elemet, akkor kiértékelte a lerakást, hogy megfelel-e a feltételeknek.
Egy készletet ez egyetlen processzoron viszonylag minimális memória használat mellett körülbelül 20 másodperc alatt értékelt ki.
A 2P és 2P1T játékok elemzéséhez még elégnek bizonyult ez az algoritmus, de a 2P2T esetén már olyan nagymértékű erőforrásra lett volna szükség, hogy ez az út nagyon lassúnak bizonyult: bizonyos optimalizálások után is 3 processzoron párhuzamosan futtatva is csak az esetek kb. 12%-át tudta feldolgozni 24 óra alatt.
Így végülis a feltételek mentén több programra bontottam a feldolgozást. Az egyes modulok az előzőek outputjait fogadják, és használják inputként. Az egyes modulok:
- nonomino lista: előállítja a 9 db csempéből álló összes kötött (9.910 db) nonomino-t, ezek szimbolizálják a játékban egy szín által alkotott 9 csempés alakzatot
- "azonos" nonomino-ból előállítható 18 csempés alakzatok: minden nonomino mellé lehelyezi önmaga vagy tükörképe valamilyen elforgatottját (0/90/180/270) minden lehetséges módon (865.488 db)
- 18 csempés nonomino párok lefedése színmentes 2 db P és 2 db T segítségével: lehelyez egy P alakaztot egy fix méretű játéktérre, és a többi három elem különböző pemrutációit különböző elforgatások (0/90/180/270) mellett hozzá illeszti. Csak azokat a lerakásokat fogadja el, amelyek megegyeznek valamely 18 csempés nonomino pár által képzett alakzattal (54.119 db lerakás). Az egyes lerakásokat hash szerű csoportokba osztotta, ahol az egyes csoportok a P és T alakzatok "állása" szerint homogének voltak.
- 2P2T lerakások színezése: az előállt 54.119 lerakási minta szerint vette az összes játszható 2P2T készletet, és az "állásuknak" megfelelő lerakások szerint megnézte, hogy van-e megoldása az adott készletnek. Ez az elemzés kb 90 perc alatt lefutott már.
Kiss Zoltán (svin)