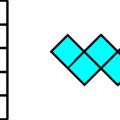
Mostanában sokszor gondolkodom a a különböző játékok nehézségén. Mitől függhet? Vannak-e határai? Érdemes-e olyan játékokat kitalálni, amelyek megoldására, elsőre úgy tűnhet, hogy esély sincs? Kísérletet sem teszek ezen kérdések megválaszolására, de a most bemutatandó játékok is komoly dilemma elé állítottak. Esélyem sem volt a megoldásukra, minden kísérletem rettentő távol állt a helyes megoldástól. Másrészt viszont látszólag nagyon egyszerű elemekből állnak, mindössze 4 L-ből. Az L-ek közül 2 pentominó és 2 tetrominó. Az egyik oldaluk:
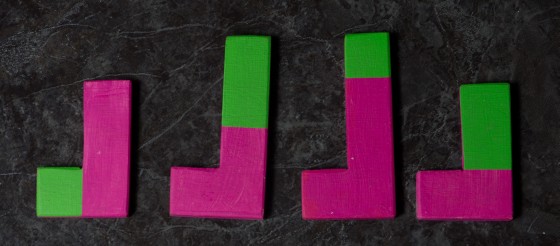
Minden elemet a helyén hagyva, de átfordítva a másik oldalra:
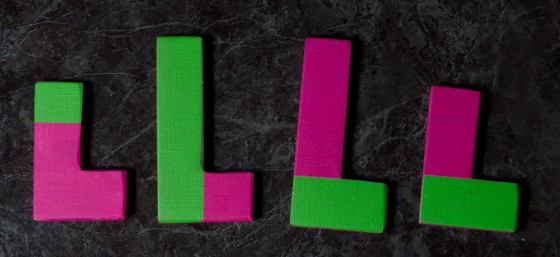
Látható, hogy két színnel vannak befestve és különböző a két oldaluk.
Ha egymás mellé helyezzük őket, különféle érdekes és bonyolult alakzatok jönnek létre a két színből. Pl a következő képen a zöld alakzat összefüggő, míg a rózsaszínű nem:
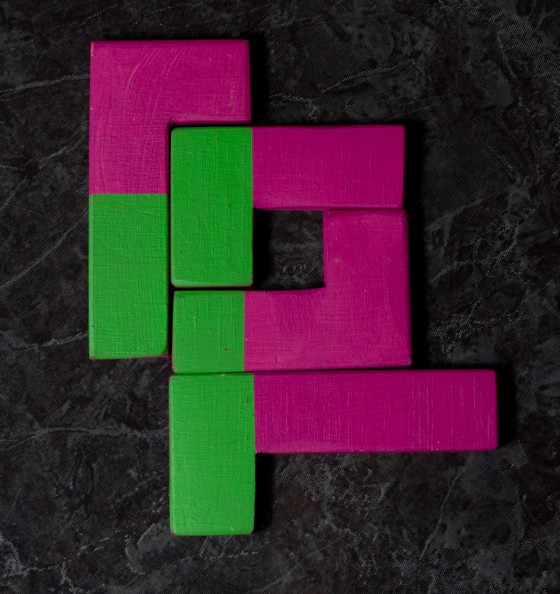
Már azt sem könnyű elérni, hogy mindkét alakzat összefüggő legyen, de hol van ez még a végső céltól!
Megfogalmazni azt sem bonyolult: érjük el, hogy a két különböző színű alakzat nemcsak összefüggő, hanem egybevágó is legyen! Vagyis a zöld és a rózsaszínű 9 kis négyzetből álló alakzatok egymással fedésbe hozhatók legyenek. Ugye, nem is hangzik annyira bonyolultan?
A 4 elem megtervezéséhez három emberre volt szükség :) Az alkotók: Tadao Kitazawa, Mineyuki Uyematsu és Keiichiro Ishino. Mindhármuk neve jól cseng az ördöglakatokkal foglalkozók között. Ishino üzemelteti a remek ördöglakatos honlapot, Uyematsu pedig rendszeres versenyző az IPP-ken, többszörös díjnyertes.
Néhány helyre elvittem bemutatni ezt a játékot, jópáran kipróbálták már, de még soha, senki nem tudta megoldani. Pedig csak 4 viszonylag egyszerű elemből áll. Persze egy ilyen bemutatón általában nem tölt senki órákat egy-egy játékkal (tisztelet a kivételnek). Én mégis azt gondolom, hogy valahol itt lehet a határa annak a bonyolultságnak, nehézségnek, amit még érdemes egy játéknak elérnie.
Egy negyedik japán úr Naoaki Takashima, aki szinte állandó vendége az IPP-knek, részt vett a játékok cseréjén is, ehhez hasonló, de nem ugyanez volt a cserejátéka. Az is 4 színes L-ből állt:

Illetve a másik oldalak:

Engem meglepett, hogy a cserejáték az összetettebb, nem pedig amit a versenyre is benevezett. Ezekből az L-ekből kétféleképpen is lehet egybevágó alakzatokat létrehozni.
Ezek a játékok nem túl nehezen elkészíthetők. (Bár az enyém nem lett túl szép, nem tudok festeni.) Valószínűleg készítek egy festés nélküli változatot is, többféle fa összeerősítésével. Ha az olvasó nagyon nehéz fejtörőt szeretne, akkor itt az alkalom, készítse el ezt!
Akár papírból kivágva, kiszínezve is játszható, de hogy még könnyebb legyen, elkészítettem a letölthető változatot is. Ha valaki nagyon pontosan tud egy papír két oldalára nyomtatni, az nyomtasson kétoldalasan és akkor egyszerűen ki kell vágni az elemeket. Ha ez nem sikerül, akkor inkább két külön lapra kell kinyomtatni a két oldalt, kivágni majd összeragasztani az elemeket. (A játékokhoz természetesen jó a fekete fehér nyomtatás is, de én színesben készítettem el.)
A rajzok letölthetők innen.
Nagyon kíváncsi vagyok, hogy az olvasók közül sikerül-e valakinek megoldani ezeket a fejtörőket. Ha igen, kérem értesítsen, és egy pár mondatban írja le a megoldás menetét!