Talán a világ legismertebb játéka a kínai tangram. Bár nem ősi, mint a hozzá fűződő legendák tartják, de elég szép múltra tekint vissza. Nekem legjobban a tangramból kirakható paradoxonok tetszenek, de mindenki megtalálhatja a számára kedves figurákat.
Van aki még tovább megy, és nagyon érdekes módosítást hajt végre az elemeken, mindegyiken "torzít" egy kicsit. A kép bal oldalán az eredeti kínai tangram látható, a jobb oldalon pedig Bernhard Wiezorke változata látható:

Mintha a jobb oldali tangram szét lenne húzva! És valóban, Wiezorke egy geometriai transzformációt, nyújtást alkalmazott a négyzet alakban összerakott elemkészletre. Egy rajzon talán jobban látszik:
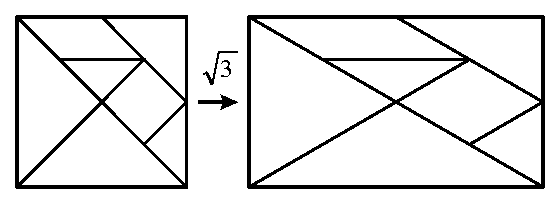
Minden vízszintes méretet megnövelt √ 3 -szorosára. De miért pont ilyen fura mértékben? Pl. trigonometriai eszközökkel belátható, hogy így az eredeti tangram 45-90-135 fokos szögei átalakulnak 30-60-90 fokossá, így ismét "szép" alakzatokat kapunk. Egyenlő oldalú, szárú háromszögeket, 60 fokos rombuszt stb. Érdekes, hogy az eredeti játéknak két-két egyforma eleme volt, ebben a transzformált játékban pedig nincsenek egyforma elemek. A kínai tangramban minden elemnek volt valamilyen szimmetriája, az újban pedig van egy, aminek semmilyen sincs. Ezek alapján sejthető, hogy az új játék, a Trigo tangram egy kicsit nehezebb, mint az eredeti.
De lássuk, hogy milyen feladványok tartoznak ehhez a játékhoz! Első ötlet, hogy a kínai feladványait is transzformáljuk, azok majd ezzel is kirakhatók lesznek. Van is, ami működik. Pl.: a gólya átalakul daruvá:

Vagy a macska rózsaszín párduccá:

Más alakzatoknál nem ennyire egyszerű a helyzet. Egy kicsit módosítani kell az elrendezésen, hogy ismét értékelhető legyen az eredmény. Így lesz a futó gyerekből korcsolyázó hölgy:

Van amikor viszont hiába próbálkozunk egy kis átrendezéssel, nem nagyon jutunk eredményre. A sapkás srácból mi lett?

Egy bizonyos szintig járható út a régi feladványok átalakítása, de nagyon sok alakzat, ami a kínaival jól nézett ki, az új készlettel már ki sem rakható, vagy nagyon fura lesz. Érdemes tehát megpróbálni kitalálni új formákat, ez talán még jobb móka, mint mások által alkotottakat kirakni!
Érdekes matekos kérdés a Trigó tangramból készíthető konvex alakzatok megtalálása. Az első képen látható téglalap konvex. És könnyen látható, hogy szétbontható két háromszögre, amiket egymásmellé pakolva szintén konvex alakzatokat kapunk. Az első:

Második:

És még egy:

Biztosan (?) léteznek még más kirakható konvex alakzatok is. Tudomásom szerint még nem vizsgálták ezt a kérdéskört. Érdekes lenne, ha megtalálnánk minél többet a kirakható alakzatok közül. Ha az olvasó küld képet, rajzot az általa találtakról, szívesen megosztom! Hátha sikerül közösen valami nagyobb újdonságot találni!




