Mindig nagy örömmel tölt el, ha egy játékot továbbgondol valaki, új lehetőségeket fedez fel benne. Most is egy ilyen vendégposzt következik!
Egyik kollégám mutatta meg nekem a Hiroshi Yamamoto által kitalált Ex 3 összerakós játékot. Nem volt egyszerű kirakni, jól elszórakoztam vele. Felmerült bennem, hogy van-e esetleg több lehetséges szimmetrikus kirakási módja a három darabnak, de nem találtam rá az interneten sem hivatkozást. Ezért úgy döntöttem, hogy megpróbálom számítógéppel megkeresni a kirakható szimmetrikus alakzatokat.
A számítógép számára először is pontosan le kell írni az alakzatokat. A síkidomok szögei szemmel láthatóan a 45° többszörösei, tehát ezzel nem volt gond. Viszont nem találtam meg sehol a pontos méreteket, így egyszerűen egy vonalzóval lemértem az oldalakat. Már első látásra is könnyen megállapítható, hogy ha a legkisebb alakzat rövidebb oldalait a-val jelöljük, akkor a síkidomok oldalahosszai a következők lesznek (az olvasóra bízzuk, hogy kitalálja melyik szám melyik élekre illik): a, √2a, 2a, (1+√2)a, 2√2a, (2-√2)a. Ennek megfelelően vettem fel a síkidomok koordinátáit a programba, de mivel nem akartam formális számokkal számolni, ezért az összes programbeli számolásnál és ellenőrzésnél figyelembe vettem a gép dupla pontosságú számfelbontásából adódó lehetséges kerekítési hibákat.
Ezután ki kellett találnom egy megfelelő algoritmust a program számára, amivel végigpróbálgathattam az alakzatok összes lehetséges összeillesztését. Mivel az egyetlen általam ismert szimmetrikus alakzat esetén a kiinduló síkidomok a csúcsaiknál illeszkedtek, ezért ezt belevettem a programba feltételnek (amit persze nem tehetnék meg, hiszen ez csak egyszerűsítése a problémának, a Symmetrick esetében például nem is lehet szimmetrikus alakzatot ezzel a feltétellel kialakítani). Hogy egyszerűsítsem a dolgomat, a csúcsokat az óramutató járásával ellenkező irányú sorrendben vettem fel, és a számolás során kialakuló alakzatoknál is mindig ezt a sorrendet tartottam. Első ránézésre így egyszerű volt végigpróbálni az összes esetet: ha már kialakult valamiféle alakzat, akkor ahhoz úgy vehetek hozzá egy újabb síkidomot, hogy az új síkidomot 45°-al és annak többszöröseivel elforgatva (8 eset), illetve az alakzatot tükrözve (2 eset) az aktuális alakzat minden csúcsát megpróbálom illeszteni az új síkidom minden csúcsához (síkbeli eltolás) és ellenőrzöm, hogy nincs-e átfedés az alakzat és a síkidom között. Menet közben több problémába is ütközünk. Ha kialakul (mondjuk egy 45°-os és egy 135°-os szögű csúcs megfelelő illesztésével) egy egyenesszög, akkor a közös csúcs eltűnik és két csatlakozó él eggyé válik. De ugyanez a probléma akkor is, ha egy teljes szög alakul ki, sőt, akkor az oldalél közös darabja is eltűnik. Ezek nyilván lekezelhető, nem túl nehéz feladatok.
Ha már kialakult a végső, mindhárom darabot tartalmazó alakzat, akkor ellenőriznünk kell, hogy szimmetrikus-e. Mivel amúgy eddig is csúcsokkal dolgoztunk, elég logikusnak tűnt, hogy csak a csúcsok szimmetriáit ellenőrizzem a következő módon. Vegyük az alakzat első (tetszőlegesen kiválasztott) csúcsát próbáljuk meg megtalálni a szimmetrikus párját, vagyis minden más csúcsra ellenőrizzük, hogy ha az a két csúcs állna szimmetrikusan, akkor az ezek által meghatározott tengely esetén az összes többi csúcshoz is megtaláljuk-e a szimmetrikus párját. Ha igen a válasz, akkor persze az alakzat csúcs-szimmetrikus és készen vagyunk. Ha a válasz nem, akkor az még jelentheti azt, hogy az első csúcs magán a tengelyen volt (tehát nincs szimmetrikus párja), így ismételjük meg az eljárást a második csúcsra is. Ha ott igen a válasz, akkor készen vagyunk, ha nem, akkor a második csúcs is a tengelyen kell legyen. Ebből már megkapnánk a tengelyt, de (mivel három, az óramutató járásával ellentétes irányban az alakzaton egymást követő csúcs nem lehet egy egyenesen) a harmadik csúccsal megismételve a fenti eljárást mindenképpen meg kell találnunk a tengelyt, ha az alakzat szimmetrikus. Így meg tudjuk találni a csúcs-szimmetrikus alakzatokat. Hozzá kell tennünk, hogy mivel csúcs-illeszkedéssel bővítjük az alakzatunkat, ezért ki kell próbálnunk a síkidomok bármilyen sorrendbeli összeillesztését, hiszen lehetnek (sőt vannak) olyan síkidomok, amelyek nem csatlakoznak egymáshoz közvetlenül.
Érdekes eredményre jutunk. Az ismert (? :) ) szimmetrikus alakzaton kívül két másikat is kapunk (pirossal az eredeti síkidomok csúcsai és élei is látszanak, a zöldnél az illeszkedő csúcsokat és éleket már kiszedtük, és a tengelyt berajzoltuk).
Az első:
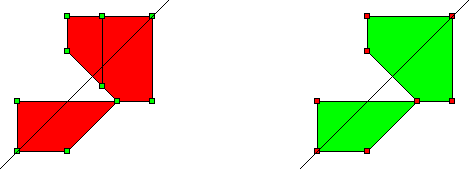
És a második:
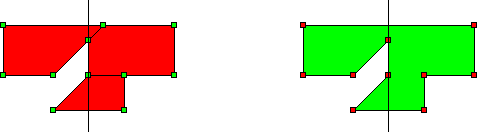
Ezeknek az alakzatoknak érdekes tulajdonsága, hogy bár a csúcsaik szimmetrikusan helyezkednek el, maguk az alakzatok nem szimmetrikusak. Ellenőrizhetnénk persze a teljes szimmetriát is (elegendő lenne például megvizsgálni, hogy ha két csúcs éllel össze van kötve, akkor a szimmetrikus párjuk is), de pontosan ez a “pongyolaság” a programban vezetett ilyen érdekes alakzatokhoz.
Makay Géza
A csúcsok szimmetriáját annyira nehéz észrevenni, hogy akár olyan játék is nehéz és érdekes lehet, ami mindössze két darabból áll. Az első ábrát tekinthetjük úgy is, hogy az két darab csúcsban érintkező elemet ábrázol, így ez felfogható egy új, két darabos fejtörő megoldásának is. Érdemes elkészíteni ezeket az elemeket!





