A közelmúltban többször tartottam ördöglakatmegoldó-versenyt. Az egyik feladat mindig az volt, hogy azonos alakzatokat kellett kirakni pentominókból. Kissé meglepett, hogy mennyi problémát okozott ez, alig-alig született megoldás. Valószínűleg alábecsültem e játéktípus nehézségét. Már foglalkoztunk vele itt, de kaptam olyan visszajelzést, hogy az a poszt "kissé" tömény, nehezen feldolgozható. Ráadásul nagyon kevesen rendelkeznek két pentominó készlettel, az ott szereplő táblázatokhoz viszont annyi kellene.
Kicsit egyszerűsítettem az adathalmazokon, ennek néhány eredménye következik most.
Ha van egy pentominó készletünk, akkor felmerül, hogy hogyan lehet kettéosztani, úgy, hogy a két félből minél több azonos alakzatot lehessen kirakni. Tekintsük a következő bontást:

Vagyis az egyik csoportban legyenek az F, I, L, P, Y, Z elemek, míg a másikban az N, T, U, V, W, X.
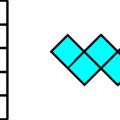
A cél minél több azonos alakzat kirakása úgy, egy-egy alakzathoz csak az egyik csoportból veszünk elemeket. Pl. a bal oldalról az FLP, jobbról pedig az NUV elemeket kiválasztva készíthető két azonos alakzat, mint az a következő képen is látható:

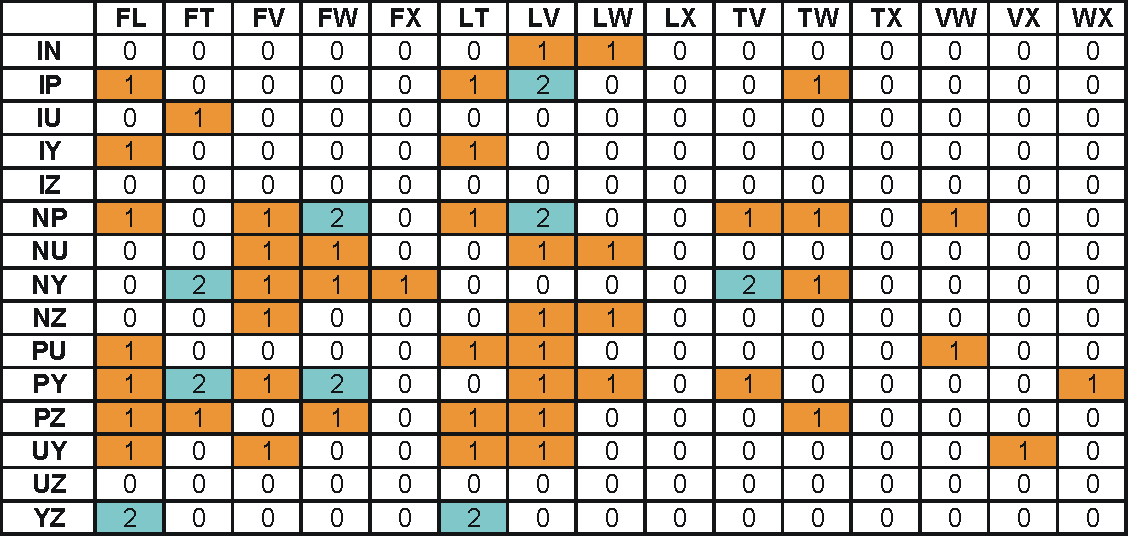
Mindkét csoportban 6-6 elem található, ezekből 20-20 darab 3 elemű részcsoportot lehet képezni. Vagyis összesen 400 lehetőség lenne azonos alakzatok kirakására. Ezek közül azonban jónéhány esetnek nincs megoldása. A fenti képen látható bontás 248 megoldható elrendezést eredményez, ezek közül 101-nek csak egyetlen megoldása létezik. Ebből a szempontból ez a bontás a rekorder.
Hogy melyik elrendezéseknek van megoldása? Ez látható a következő ábrán:
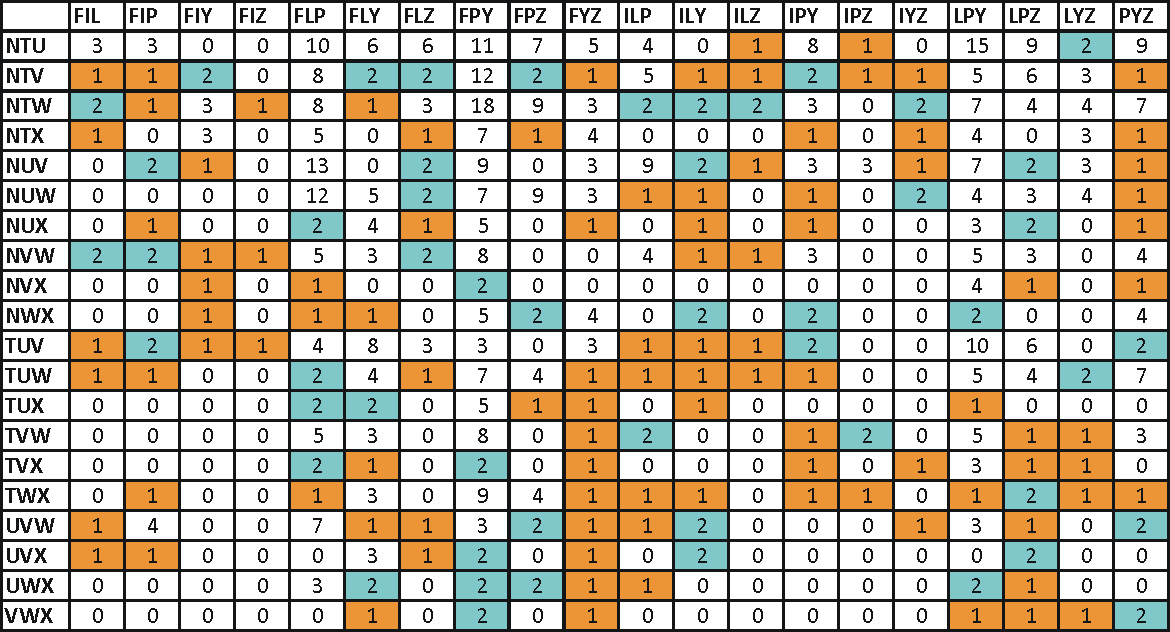
Már ez a táblázat is elég sok gondolkodni valót kínál, de azért álljon itt egy másik bontás is:

Tehát az egyik csoportban az ILNPTU elemek találhatók, a másikban pedig az FVWXYZ.
Ez a felosztás semmilyen különleges tulajdonsággal nem rendelkezik, nagyjából véletlenszerűen választottam. De ennek is van több mint 200 megoldható feladványa, amik közül 69 csak egy megoldással rendelkezik. A hozzá tartozó táblázat:
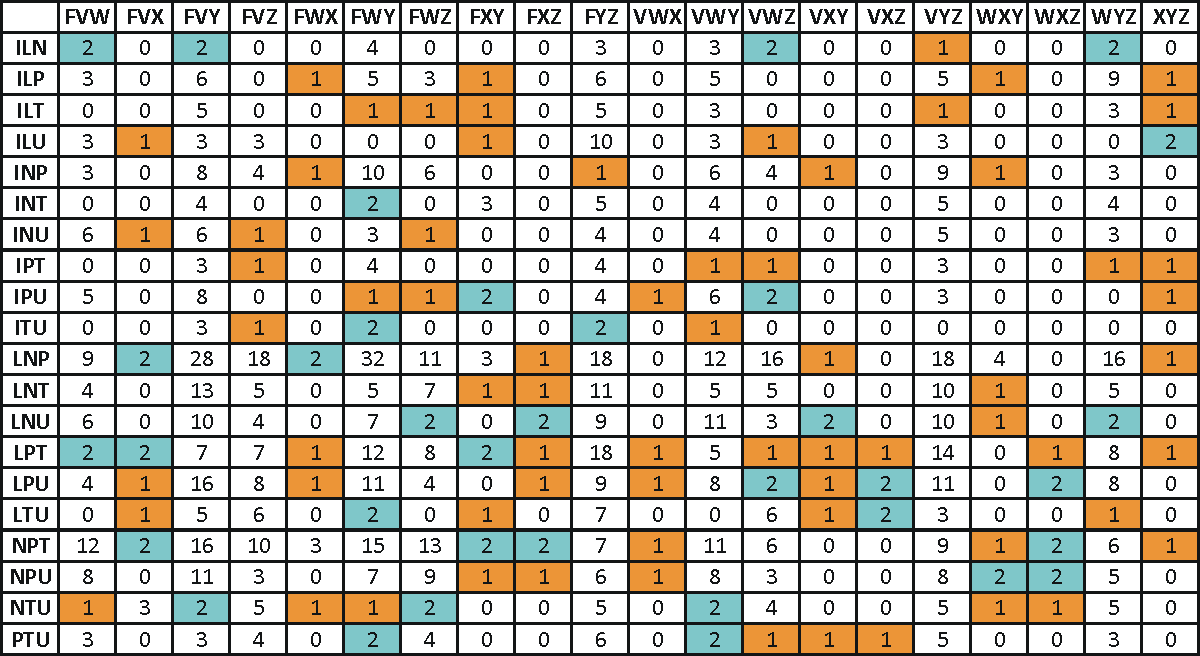
Ismét meg kell jegyeznem, hogy ezek elég nehéz feladványok. Nagyon sokaknak beletörik a bicskája.
Lényegesen egyszerűbbek a 2-2 elemből készíthető azonos alakzatok. Pl. egy bontás:
És két-két elemből kirakva egy azonos alakzat:

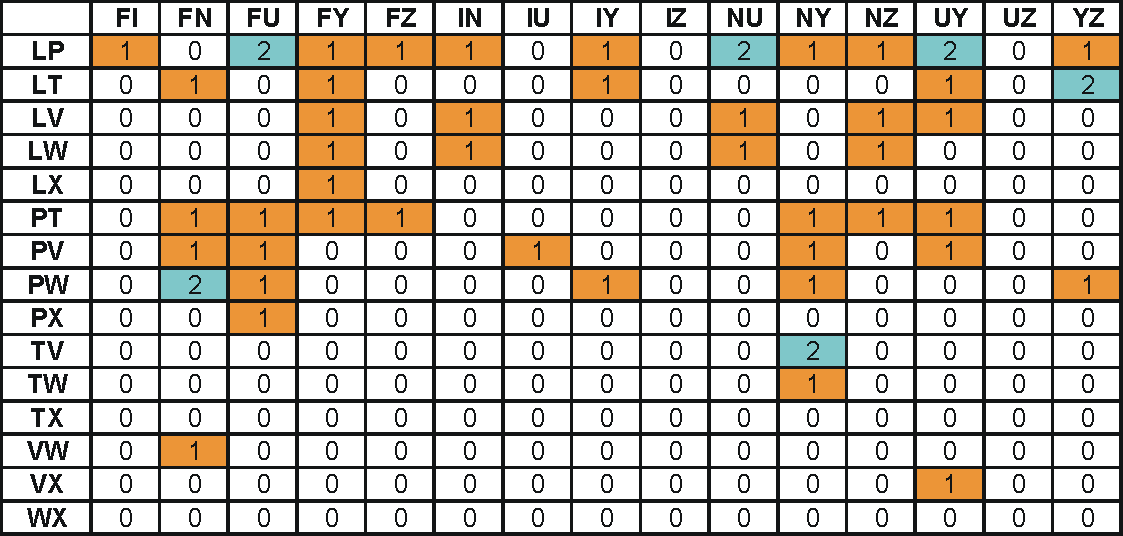
A 6-6 elemből 15-15-féle módon lehet kiválasztani, így most 15×15-ös táblázatokat kapunk. Az ehhez a bontáshoz tartozó:
A 225 lehetséges esetből 55 megoldható, ezek közül 46-nak egy megoldása van, a többinek kettő. Ez a legnehezebb.
Még egy, véletlenszerűen választott bontás:

A táblázata:
Végezetül egy elsőre meghökkentő feladvány!
Ha megvizsgáljuk a legelső táblázatot, akkor láthatjuk, hogy az FLZ és a TVW elemekből nem lehet azonos alakzatot kirakni. Megváltozik azonban a helyzet, ha áttérünk 3 dimenzióba:

Nemcsak az elemek lehetnek 3 dimenziósak, hanem a kirakandó alakzatok is. Így már megoldható feladványt kapunk. Méghozzá olyat, ami a legnehezebbek közé tartozik! A nagyon kitartó és türelmes játékosoknak javaslom csak!
Próbáltam olyan 2-2 darabos 3 dimenziós készleteket is találni, amiknek síkban nincs megoldásuk, de térben van. Sajnos nem jártam sikerrel. Örülnék, ha valaki rábukkanna egy ilyenre és ezt megosztaná velem is!
A bejegyzésben szereplő táblázatok megformázva, kis magyarázó szöveggel letölthetők innen.