Nem, most nem ufókról vagy más földönkívüli dolgokról lesz szó, csak folytatjuk a 6 elemű rabkereszteket bemutató sorozatot. Az alapokról szóló bejegyzésben már szerepelt a típus fogalma. Ott is és az előzményekben is csupa 1. típusú keresztet ismertettem. Mindegyikben szerepelt a tömör, bevágásokat nem tartalmazó rúd, azt pedig az első lépésben el lehet távolítani az összerakott keresztből.

Most áttérünk bonyolultabb esetek tárgyalására. Egy magasabb típusú kereszt látható a következő képen, már majdnem teljesen összerakva:

Egy rabkereszt típusa tehát az a szám, ahány elemet lehet egyszerre eltávolítani az összerakott játékból. Másképp fogalmazva: szétszedéskor egy rabkereszt előbb-utóbb két csoportra különül el. E csoportok közül a kisebbik elemszámát hívjuk típusnak.

Tekintsük az alábbi elemkészletet:

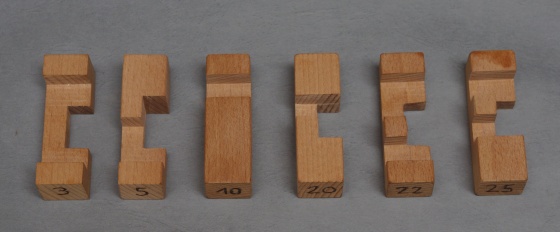
Megpróbálhatunk ezekből egyesével összerakni egy keresztet, már majdnem elkészülünk, amikor valami ilyesmi állás alakul ki:

Látjuk, hogy ez az utolsó elem elférne a keresztben, de így képtelenség berakni. A megoldás, hogy ezt az utolsó elemet már a behelyezés előtt összeépítjük az utolsó előttivel:

Így a két elem együttesen már behelyezhető a másik négy közé. Mivel egy 2-es és egy 4-es elemcsoportot kell kialakítani az összerakás során, ez a kereszt 2. típusú.

Érezhető, hogy az egynél  magasabb típus egy újabb bonyolítást hoz a játékba. Nemcsak az elemek elhelyezkedését és sorrendjét kell kitalálni, hanem ezek csoportjait is.

Lássunk példát más típusra is! Az alábbi elemek 3-as típusú keresztet eredményeznek:

Ezeknek az összerakás előtti állapotát már lefényképezni sem volt egyszerű, nem nagyon állnak meg maguktól az összerakott elemcsoportok. Ez az összeállításnál is problémát okoz, nem ártana egy 3. kéz, amivel az első három elemet tartjuk, amíg a második hárommal küzdünk. A végső összeállítás előtti pillanat:

Ezek az elemek láthatók csaknem teljesen összeállítva az első képen.

Stewart Coffin, az egyik legnagyobb logikaijáték-tervező is foglalkozott a magasabb típusú keresztekkel. Talált két nagyon érdekes elemkészletet (az alapoknál említett Bill Cutler eredményeit felhasználva.)

Coffin első készlete:

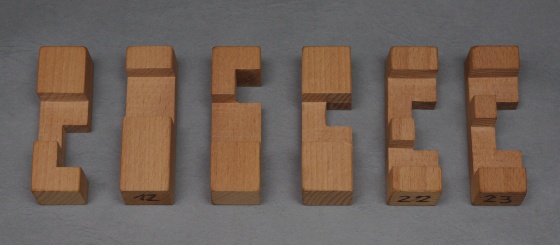
És a második:

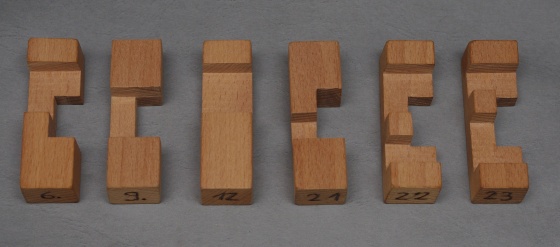
Mindkét kereszt csupa olyan elemből áll, amik semmiféle térbeli forgatási szimmetriával nem rendelkeznek, így rendkívül nehéz megtalálni a helyes állásukat. Coffin számításai szerint e két kereszt a legnehezebb a belül tömörek (és fűrészelhető elemekből állók) közül.

A jó megfigyelő olvasó talán már észrevette, hogy a két utolsó elemkészlet mindössze egy elemben tér el. Így, ha valaki rendelkezik a két utolsó képen látható összesen 7 elemmel, akkor a két (bizonyos szempontból) legnehezebb keresztet tudhatja magáénak.

És, hogy mik azok a számok az elemekbe égetve? A legközelebbi 6 elemű rabkeresztekről szóló bejegyzés pont erről fog szólni.