A pentominók négyzetekből állnak, a tetrahex játék elemi hatszögekből épülnek fel. Korábban volt már szó "vonalzókból" álló elemekről is. Most egy olyan játékot mutatok be, aminek elemei szabályos háromszögek összeerősítésével keletkeznek.

Hat szabályos háromszöget 12-féle módon lehet teljes oldaluknál összekapcsolni, ez a 12 alakzat alkotja a Hexiamond játékot.

Az elemek:

Hogy a háromszögek elhelyezkedése jobban látható legyen, következzen most ugyanez rajzban is:

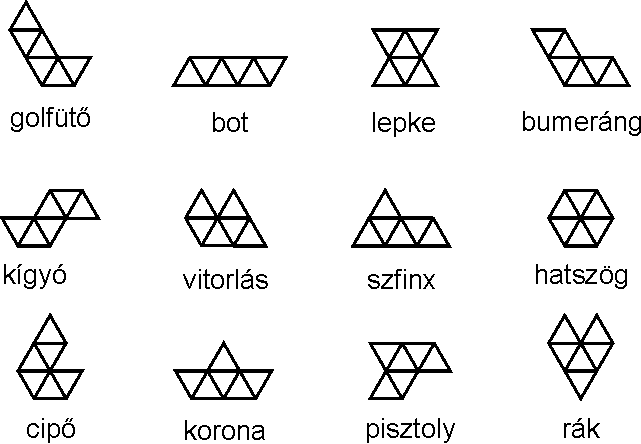
Az elemek az alakjukra emlékeztető tárgyakról kapták a nevüket, könnyebb így hivatkozni rájuk.

De honnan jön az egész játék elnevezése, a Hexiamond? A két háromszögből álló alakzat hasonlít egy gyémánt sematikus rajzához. A gyémánt angolul: diamond. Bár ebben a kifejezésben a "di" szótagnak semmi köze nincs görög "kettő" előtaghoz, a hangzása mégis azonos. Ez adta az ötletet, hogy a hat háromszöges elemek nevében az előtag legyen a "di" helyett "hex". Így lett a gyémántból egy kirakós játék :)

Érdemes megjegyezni, hogy a szabályos sokszögek közül csak a háromszöggel, négyzettel és hatszöggel lehet lefedni a síkot. Így, ha olyan játékot akarunk készíteni, amiben hézagmentes alakzatok is kirakhatók, ráadásul az elemeket egyforma alakzatok összekapcsolásával szeretnénk előállítani, csak e három szabályos sokszögből indulhatunk ki. A vonalzós játék nem szabályos sokszögekből épül fel, de azokkal is lefedhető a sík. A későbbiekben fogunk még egyéb érdekes sokszögeken alapuló játékokkal is találkozni.

De miket is lehet kirakni ezekből az elemekből? Csak a fantázia (és az ügyesség) szab határt a szép alakzatok keresésének.

Egy ülő kutya:

Vagy egy tengelyesen szimmetrikus forma, mondjuk egy lopakodó:

Elég nehéz feladat a különböző, kevés szimmetriával rendelkező elemekből szimmetrikus alakzatokat kirakni. Ha jól tudom, a mai napig megoldatlan probléma a Hexiamondokból kirakható szimmetrikus formák számbavétele. Kicsit könnyebb a konvex alakzatoké, de e témakör teljes elemzéséről sincs tudomásom.

Azt azért tudjuk, hogy lehetséges konvex formákat kirakni! Következzen egy rombusz:

A rombusz is paralelogramma, de vajon lehet-e a fentin kívül más paralelogrammákat kirakni az elemekből? Esetleg nem az összes hexiamond-ot felhasználva? A válasz pozitív, lehet kísérletezni!

Következzen még egy szép, 6-os forgásszimmetriával rendelkező alakzat, egy csillag:

Esetleg sikerül az olvasónak másfajta szimmetriákkal rendelkező formákat is kirakni?

A Hexiamond elég nehéz játék, aminek oka az elemek viszonylag szokatlan formájában kereshető. Bár a 12 különböző elem nem túl sok, mégis elég komoly fejtörést ígénylő feladványokhoz is. Érdekes, hogy pont 12 a hexiamondok és a pentominók száma is. Nem tudom, van-e ennek valami mélyebb oka. Általában a hasonló játékok elemszáma nagyon nehezen meghatározható.

7 háromszöget már 24 különböző módon lehet összeerősíteni, ami túl sok egy játékhoz, de mint matematikai, számítástechnikai probléma érdekes lehet.

Folyik a kutatás a különböző számú háromszögekből álló alakzatok mennyiségének meghatározására. Talán meglepő, de ma még csak 30 háromszögig tudjuk a választ: 30 háromszögből 647.943.626.796-féle alakzat készíthető. 

Javaslom az olvasónak, hogy próbáljon készíteni magának egy Hexiamon készletet, mivel boltban nagyon nehezen beszerezhető. Rendkívül sok problémát lehet találni és kitalálni e játékhoz: a nehéztől egészen az önálló kutatási témákig.