Már többször foglalkoztunk pentominók felcserélhetőségével. Ebben a bejegyzésben kétféle pentominóból kellett ugyanazt az alakot kirakni, itt pedig 3-féléből. Felmerül a kérdés, hogy mi a helyzet akkor, ha az egyik elemcsoport nem pentominókból áll, hanem más poliominókból. (A poliominók a négyzetek összeerősítésével keletkező alakzatok.)

De mekkora lehet az az alakzat, amit az 5 négyzetből álló pentominókból és a 4 négyzetből álló tetrominókból is ki lehet rakni? Nyilván 5-tel és 4-gyel is oszthatónak kell lennie a területének, így minimum 20 négyzetből kell álljon. Nem biztos, hogy ez elég, de legalább ekkora kell legyen.

Milyen alakzatot lehet kirakni pl. néhány F pentominóból és T tetrominóból?

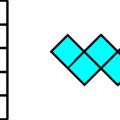
Tudjuk, hogy legalább 4 F-re és 5 T-re lesz szükség. De vajon elég-e ez? Amint a következő kép mutatja, elegendő:

Bár a minimális elemszámot kell csak felhasználni, mégsem egyszerű feladat ez, sőt!

Az F pentominóból minden tetrominóból kirakható ugyanaz az alakzat. Ehhez általában elég a minimális elemszám (vagyis 4 és 5), kivéve a legegyszerűbb tetrominót, a 2×2-es négyzetet, amiből 10 darabra van szükség. Próbáljon meg az olvasó néhány megoldást megtalálni!

Ha készítünk egy nagy táblázatot, aminek a sorait a pentominók jelzik, az oszlopait a tetrominók, akkor annak 12×5=60 mezője lesz. Ezekbe a mezőkbe rajzolhatjuk be a közös alakzatokat. Vagyis ez a játék 60 feladványból áll. Szerencsére(?) a táblázat nagy része tényleg kitölthető. Összesen 2 mező van, amik megoldhatatlan problémát jelölnek. Nem lehet azonos alakzatot kirakni az X pentominóból és a négyzet tetrominóból. Vagy az X-ből és az egyenes tetrominóból.

Érdemes megkeresni néhány megoldást. Nagyon szépek vannak köztük. Az én személyes kedvencem a T pentominó és T tetrominó által alkotott pár. Ehhez is csak 4, ill. 5 elem kell, de jópofa szimmetrikus alakzat a megoldás. Érdekes még a P pentominó és a négyzet párosa. Ehhez ugyanazt az alakzatot kell kirakni, mint amit a Penrose parkettázásról szóló cikkben is láttunk.

De kisebb, kevesebb elemet igénylő feladványok is léteznek, csak akkor nem a tetrominókat kell párba állítani a pentominókkal, hanem pl. a triominókat. Minimum 3 pentominóra és 5 triominóra van szükség, de pl. a T és az L párhoz ez nem elég:

Kétféle triominó létezik, így az előbb vázolthoz hasonló táblázat most 12×2 mezőből áll. Ennek csak 1 mezője nem tölthető ki, méghozzá megintcsak az X és az egyenes triominó mezője. Ezek már lényegesen könnyebb feladványok, de azért itt is akad pár elgondolkodtató eset.

Kicsiknek és kezdőknek érdekesek lehet a pentominó-dominó párosítások. Ezekhez minimum 2 pentominóra és 5 dominóra van szükség. És az X pentominót kivéve ennyi elég is. Az X-es eset is megoldható, de ehhez 4 darab X-et kell felhasználni és 10 dominót.

Ha nincs is az olvasónak ennyi pentominója, tetrominója..., akkor is érdemes néhány esetet papíron kipróbálni. Esetleg kivágni az elemeket. Nehéz feladványok ezek, de jó szórakozást ígérnek.