Janus a római mitológia kétarcú istene. Arcai egyszerre tekintenek a múltba és a jövőbe, a nyitás és a zárás felé, de egyszerre figyelik a kezdetet és a véget is.

(A kép innen származik.)
Janus két arca teljesen egyforma, nincs szebb vagy jobb oldala, nem ad útmutatást a helyes irány kiválasztásához. A Janus-arcú kifejezés kissé elszakadt az eredeti jelentéstől, ma már inkább kétszínű, egymásnak ellentmondó értelemben használjuk. A következőkben ismertetett játék is ezen új értelmezés alapján kapta a Janus nevet.
Egy kétdimenziós összerakó játék elemeinek általában egyforma a két oldala. Pl. az általam készített kínai tangram minden elemének mindkét oldala egyszerűen natúr fa erezetű.A paralelogrammán kívüli elemek esetén nincs is jelentősége a két oldal mintázatának, hisz tengelyesen szimmetrikusak, így átfordíthatók a másik oldalukra.
A sok azonos elemet tartalmazó játékokat feldobhatja a színezés, ezáltal új feladványok születhetnek, vagy már létezők nehezedhetnek meg. A legjobb példa erre a Színdominó, ami nem is lenne fejtörőnek nevezhető színek nélkül.
Egy korábbi bejegyzésben részletesen foglalkoztunk azonos elemekből kirakható téglalapokkal. Ott csak az elemek formája számított, egyik sem volt színezve. Szerepelt ott a 10 darab Y pentominóból kirakható téglalap. Ez önmagában nem nehéz feladvány, több-kevesebb próbálkozással bárki megtalálhat egy kirakást. Sőt, a türelmesek akár az összeset is, hisz mindössze négy lényegesen különböző létezik:
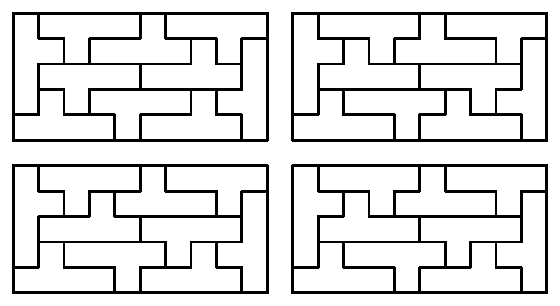
Az összes többi elrendezés ezek közül valamelyiknek az elforgatott vagy tükrözött változata.
Színezzük ki pl. a bal felső elrendezést, de úgy, hogy a szomszédos elemek különböző színűek legyenek! Könnyen látható, hogy ehhez elég 3 szín. Legyenek ezek a kék, a sárga és a lila. Az első két elem színét még szabadon megválaszthatjuk, a többi azonban már adja magát. Így kialakulhat pl. a következő mintázat:
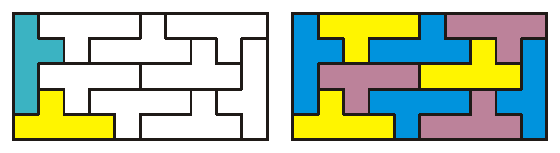
Már az is érdekes játék lenne, ha színezett Y pentominókból kellene kirakni a téglalapot. De Frits Göbel holland játéktervező még rátett egy lapáttal, és ravasz módon megszínezte az Y-ok másik oldalát is ugyanezekkel a színekkel. Hogy nehéz legyen a játék, arra törekedett, hogy egyik elemnek se legyen ugyanolyan színű mindkét oldala. Meg lehet ezt egyáltalán csinálni?
A fenti színezés átfordítottja (vagyis vízszintes tengelyre tükrözött változata) látható a következő ábrán. Az elemek most nincsenek kiszínezve, a beléjük rajzolt karika jelzi a másik oldal színét. Mivel egyelőre nem tudjuk, hogy milyen színűek legyenek a most látható oldalon az elemek, a színeket csak számokkal jelöltem:
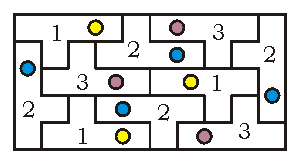
Ha azt akarjuk, hogy az elemek két oldala különböző legyen, akkor az 1-es nem lehet sárga, a 2-es nem lehet kék és a 3-as nem lehet lila. Vagyis elvben két lehetőség maradt: 1=kék, 2=lila, 3=sárga vagy 1=lila, 2=sárga, 3=kék. Ha elkészítenénk a két variációt, észre vehetnénk, hogy mindkettő ugyanazt az elemkészletet eredményezi. Így megállapíthatjuk, hogy lényegében egyféleképpen színezhetjük az elemeket és a színezés olyan játékot eredményez, aminek csak egyetlen megoldása van. Bár most a téglalap fent bemutatott 4 lehetséges elrendezése közül csak egyet vizsgáltunk, ugyanez igaz a másik 3-ra is.
No, ennyit az elméleti megfontolásokról.
Mivel volt itthon pár lézerrel vágott Y pentominóm (mindenkinél kallódik valahol egypár, nem? :)) el akartam készíteni a játékot. Már csak azt kellett kitalálni, hogy hogyan legyen látható az összerakás mindkét oldala. Ismét a könyv forma mellett döntöttem, de olyan borítót készítettem, amin egy "ablak" van, az ablak belseje pedig átlátszó:

Azért is tetszett ez a játékötlet, mert a végső, legnehezebb feladványon kívül adódik három könnyebb is. A 10 elem mindenféle megkötés nélküli elhelyezése akár kisgyerekeknek is feladható fejtörő. Viszont úgy behelyezni az elemeket, hogy mindkét oldalon stimmeljen a színezés, már komoly erőfeszítést igényel. A következő képen egy olyan elrendezés látható, ahol az egyik oldal biztosan jó:

A következő két fotón az általam használt színezés látható. Az elsőn az elemek egyik oldala:

És az elemek átfordítva a másik oldalukra:
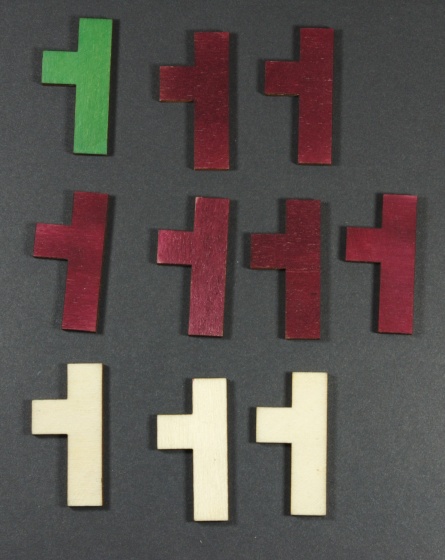
Javaslom az olvasónak, hogy készítse el a játékot! Az elemeket ki lehet vágni kartonpapírból is, és a színezéskor esetleg egy pöttyel lehet jelölni a másik oldal színét, így nem is kell átlátszó felület a kirakáshoz. Nagyon érdekes, hogy egy egyszerű ötlettől hogyan tud egy könnyű játék igazán nehézzé válni!
Ördöglakat blog a Facebookon is! Lájkoljátok, terjesszétek!




