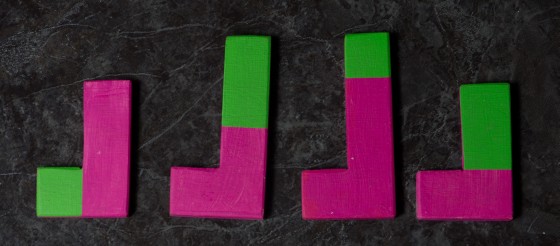Ördöglakat

Már többször foglalkoztunk pentominók felcserélhetőségével. Ebben a bejegyzésben kétféle pentominóból kellett ugyanazt az alakot kirakni, itt pedig 3-féléből. Felmerül a kérdés, hogy mi a helyzet akkor, ha az egyik elemcsoport nem pentominókból áll, hanem más poliominókból. (A poliominók a négyzetek összeerősítésével keletkező alakzatok.)

De mekkora lehet az az alakzat, amit az 5 négyzetből álló pentominókból és a 4 négyzetből álló tetrominókból is ki lehet rakni? Nyilván 5-tel és 4-gyel is oszthatónak kell lennie a területének, így minimum 20 négyzetből kell álljon. Nem biztos, hogy ez elég, de legalább ekkora kell legyen.

Milyen alakzatot lehet kirakni pl. néhány F pentominóból és T tetrominóból?

Tudjuk, hogy legalább 4 F-re és 5 T-re lesz szükség. De vajon elég-e ez? Amint a következő kép mutatja, elegendő:

Korábbi vendégposztomban is a Hanyama Cast Puzzle sorozatának néhány tagját mutattam be, ezúttal is így teszek. A gyártó a játékokat hatos skálán osztályozza nehézség szerint. Az eddig megjelent ördöglakataik közül pont hét kapta meg a legmagasabb, hatos nehézségi besorolást - ezeket a játékokat vesszük most sorra. A Cast Enigmáról már írtam korábban, a maradék hatot a saját értékítéletem szerint tettem egyre nehezedő sorrendbe, az Enigma körülbelül a lista közepére illene.

A 6-os nehézségű játékok:

A 33. IPP-n, a versenyen felbukkant egy érdekes játék. (Dehogy egy, rengeteg, de most egyről lesz szó :)) Nekem már első látásra megtetszett, hisz kevés, egyszerű elemből állt, a megoldása pedig egyáltalán nem tűnt egyszerűnek. Gyorsan el is készítettem a saját változatomat:

Látható, hogy a 4 elemből 3 egyforma (a színektől tekintsünk el). A feladvány szerint két azonos alakzatot kell kirakni az elemekből.

Nem tudom, hogy volt-e már ilyen az IPP-k történetében. Ha volt is, csak a leghíresebb, legjobb nevű játéktervezők, az igazán különleges és egyedi látásmóddal megáldott alkotók érhettek el ilyen eredményt. Az idei tervezői versenyen ismét Zagyvai András játéka kapta a zsűri nagydíját. Azt hiszem, sokan emlékeznek még a SmartEgg-re, a mai napig az arról szóló bejegyzés az egyik legtöbbet keresett írás. Az is András játéka és a most diadalmaskodó GEAPPLE is:

Fotó innen.

Ismét vendégposzt következik. Olyan oldalról pillanthatunk bele egy játék születésébe, amilyen itt a blogon még nem szerepelt. Kösz Pista!

Egyszerre vagyok kisgyerekes családapa és játékmániás. A kettő együtt veszélyes kombináció, főleg amikor játékvásárlásra kerül a sor. Próbálsz megmaradni az apa szerepében és úgy választani, hogy a gyerek képességeinek és érdeklődésének megfelelő játékot válassz. De mindig ott repked a füled mellett a kisördög és azt súgja a füledbe: „Ez lesz a jó, gondold csak el, milyen jót fogsz vele játszani.” Én abban az áldásos helyzetben vagyok, hogy a gyerekeim szívesen oldanak meg feladványokat. Így nem nehéz olyan játékot venni nekik, amivel én is szívesen játszom néha. A mai játékpiacon ugyanis meg lehet találni azokat a játékokat, amik sok feladványt tartalmaznak, különböző nehézségi fokozatokba sorolva. Ha a leírásban szerepel még néhány olyan mondat is, mint „eddig még nem megoldott probléma”, vagy „nem tudjuk, hogy létezik-e megoldása”, az a férfi fül számára a legnagyobb mézesmadzag.

Keveseknek adatik meg, hogy jelen legyenek egy ötlet játékká fejlődésénél. Valószínűleg sokaknak ez nem is jelentene olyan nagy élményt. Ha viszont a fent említett játékmániás apukáról beszélünk...

Megadatott az a különleges élmény, hogy figyelemmel kísérhettem, ahogy Péter egyik ötletéből játék formálódott. És most nem a fűrészelésről, csiszolásról és ragasztásról beszélek, hanem a szellemi alkotás folyamatáról. Rendszeres olvasója vagyok a blognak, így tudom, hogy van a visszajárók között olyan, aki pontosan tudja miről beszélek. A többieknek próbálok néhány momentumot felvillantani, ahogy nagyanyám szokta mondani: „az ézi kedvéért”.

Egy nap Péter azzal jött, hogy van egy ötlete és azt tervezi, hogy indul vele az IPP játéktervezői versenyén. Persze már hozta is a prototípust, hogy több társammal egyetemben kipróbáljuk. Egy sokfeladványos játékról volt szó, a fentiek alapján tehát sejthető, azonnal rákattantam.

A feladványok egy-egy lapon szerepeltek. Egy lapon két darab, fehér és fekete négyzetekből kirakott alakzat volt lerajzolva. Az egyik egy test felülnézeti képét mutatta, a másik ugyanazon test elölnézeti képét. A játék maga egységkockákból készített L-tetrominókból állt. Minden elem két sötét és két világos kockából volt felépítve. Így a lehetséges színezések száma hat. A feladat pedig a következő: a hat darab, L-tetrominóból válasszunk ki valamennyit és építsünk össze belőle egy olyan testet, amelynek a két adott nézete megegyezik a kártyán láthatóval.

Ezen a hétvégén kerül megrendezésre a már hagyományos Kutatók Éjszakája. A számos remek tudományos műsor mellett én is ott leszek rengeteg játékkal. Jópárat most először láthat a nagyközönség.

Este 8:20-tól pedig egy rövid előadást is tartok a kevés darabból álló, egyszerűnek tűnő, de igazából jó nehéz játékokról.

A számtalan helyszín közül az ördöglakatok a központi programban kapnak helyet a Dürer Rendezvényházban (Ajtósi Dürer sor 19-21).

Ismét egy pálcákkal és lyukas táblával játszható ördöglakatról lesz szó. Több hasonló szerepelt már a blogon, pl. a szoliterek vagy a Holdbéli kiszorító. Az előbbiekhez viszonylag nagy tábla és sok pálca szükséges, az utóbbi viszont egész kis táblán, kevés pálcával is jó nehéz feladványokat eredményez. Nemrégiben fedeztem fel egy játékot, ami még kisebb táblán és szintén kevés bábuval játszható és bizony nekem komoly fejtörést okoztak már a kezdő feladványok is.

Egy baj azért van vele, kell hozzá néhány speciális pálca:

A speciális pálcák úgy keletkeznek, hogy némelyik végére egy korongot erősítettem. Két ilyen nem fér el egymás mellett. Csak átlósan:

Eddig nem szerepelt a blogon a most bemutatandóhoz hasonló játék. Volt már szó szögekről, de azoknak a játékoknak a szétszedése-összerakása volt a feladvány. A most következők megoldásához egy kis fizika, egy kis ügyesség és sok-sok türelem szükséges.

Na meg egy marék szög és egy talapzat:

Én 200-as szögeket használtam, de jóval kisebb is elég, akár 100-as vagy 80-as. Minimum 7 darabra van szükség, de jóval többel is megoldható a játék, sőt meglepőbb, látványosabb, ha sok szöget használunk.

Már láttuk, hogy a pentakocka készletet ki kell egészíteni tetrakockákkal, hogy nagyobb kockát tudjunk kirakni. A 3 egység oldalú kockához szükség volt mindhárom tetrakockára, a 4 egység oldalúhoz pedig 12 pentakocka és egy tetrakocka szükséges.

Adódik, hogy a 2 kockából álló dikockát is vegyük be az elemek közé, hisz a 27 egység térfogatú 3-as kockából ezt "kivonva" már 5-tel osztható térfogatot kapunk. De vajon kirakható-e így kocka? Mint a következő kép bizonyítja, a válasz pozitív:

A minap foglalkoztunk már a pentominók felcserélhetőségén alapuló feladványokkal. Olyan esetekről volt szó, amikor két különböző fajta pentominóból raktunk ki azonos alakzatokat. Már ott is előfordultak olyan párosítások, amik megoldásához viszonylag sok darabra volt szükség, A mostani feladványokhoz is sok pentominó kell, sőt más poliominókat is használunk. Szerencsére nekem ezekből is van jópár darabom, amint a pentominós dobozok körül látszik:

Ha valakinek véletlenül nem lenne ennyi, akkor sincs minden veszve, ezek az elemek nagyon egyszerűen elkészíthetők papírból is. Sőt az egyszerűbb megoldások megtalálásával akár egy ceruzával kockás papíron is lehet próbálkozni.

Mindig örülök, ha látom, hogy sikerül felkelteni mások érdeklődését egy-egy játék iránt. Az azonban meglepett, hogy talán a blog történetének legalaposabb elemzését egy vendégszerző végzi el. Lehet, hogy részletesebben, körültekintőbben járt el, mint az eredeti játék megalkotói! Legalábbis a cikk vége felé található következtetések ezt látszanak igazolni!

Az "Azonosság - L" című postból megismert játék meglehetősen egyszerűnek tűnik: könnyen elkészíthető, és a játék szabályai is könnyen érthetőek. Ugyanakkor Péter leírása alapján a megoldása nem egyszerű, sőt kifejezetten nehéz. Ez számomra egyből vonzóvá tette, és gondoltam kipróbálom magam rajta, mert a cikket olvasva ötletem is volt, hogyan kezdenék hozzá. Papírból vágtam ki a két játékot, és nekiálltam a próbálgatásnak.
A zöld-lila játékhoz találtam egy megoldást, ami később "hibásnak" bizonyult, mert a feladat leírása alapján a folytonosság kritériuma nem volt akkor egyértelmű számomra. A piros-fekete játéknak az ötletem alapján az egyik megoldását megtaláltam viszonylag hamar. Miután Péterrel tisztáztuk a folytonosság kritériumát, pár órás próbálkozás után (tényleg nehéz a játék) a piros-fekete második megoldása is meglett. A zöld-lila helyes megoldását viszont hosszas próbálkozás után sem találtam. Végül feladtam, és szoftveres elemzéssel 20 másodperc alatt meglett az eredmény. Péter javaslatára - és mivel akkor már engem is érdekelt a dolog mélyebben - nekiláttam, hogy szoftver segítségével feltérképezzem ezt a játékot.
Hány darab megoldással rendelkező készlet létezhet? Vannak könnyű és nehéz készletek? Az IPP-n bemutatott két készletben van valami különleges? Milyen lehetőségeket rejt még ez a játék?
Ezekre a kérdésekre igyekszem most választ adni.

Azonosság L játék:

Először is a feladat:
Két színnel csempézett két-két darab pento- és tetrominot kell úgy elhelyezni, hogy a létrejövő alakzatban mindkét szín összefüggő (a csempék élen illeszkednek) alakzatot alkosson, és a két szín alkotta alakzatok forgatással és tükrözéssel egymásba transzformálható legyen.

Íme egy példa, ahol a fehér és a piros csempék alkotta alakzatok "azonosak":

és a megoldása:

Idén ismét megrendezésre kerül az immár hagyományos Ördöglakat találkozó. A helyszín, mint az eddigi 7 évben mindig, Bakonysárkány.

Ebben az évben két külön "verseny" is lesz. Egyrészt a - már szintén hagyományos - ördöglakat, logikai játék tervezői pályázat. Ezen kívül lehet pályázni egy érdekes konkrét tárgyból készült játékkal is. Szerintem ez nagyon jópofa ötlet.

Lassan el kell kezdeni a játékok kitalálását, elkészítését!

A fentieken kívül lesznek még érdekes előadások, ördöglakatcsere és sok-sok játék!

A nagyon jó hangulatú rendezvényen a részvétel ingyenes, sőt egy finom gulyásra is megvendégelnek bennünket. Gyertek minél többen!

A találkozó részletes leírása ezen a honlapon található.

Ugye mindenkinek van otthon egy rakás pentominója meg jónéhány tetrominója és a társai? Mert a most következő játékokhoz egy készlet nem elég, de még kettő sem. Szerencsére nekem van pár:

A pentominókról már sokszor volt szó a blogon, nem véletlenül, szerintem az egyik legsokoldalúbb játék. A kb. 100 éves történelme számtalan könnyebb és máig megoldatlan problémát rejt, így gyerekek, de akár tudósok is foglalkozhatnak a témával. Érdemes elolvasni az előbb linkelt bemutató bejegyzést, az ott szereplő elnevezéseket fogjuk használni itt is. A most bemutatandó feladványok között lesz egész egyszerű is, de ismeretlen megoldást is keresünk!

Amikor megírtam a 9 elemű rabkeresztről szóló cikket, elterveztem, hogy lesz folytatása, mert úgy éreztem, rejt még magában lehetőségeket a téma. Az első cikkben szó volt az alapjáték születéséről, és néhány elem cseréjével kapott könnyebb-nehezebb változatokról.

A 6 elemű rabkereszteknél részletesen foglalkoztunk a hasonló játékok típusával. Ilyen magasabb típusú változatokat a 9 elemű keresztnél is sikerült találni. Talán még érdekesebbek és nehezebbek a magasabb fokozatú rabkeresztek. Ezekről is volt már szó pl. itt, vagy a rekorderekről itt. Elhatároztam, hogy a 9 elemű keresztnél is keresek magasabb fokozatú változatokat.

Erről az alakzatról van szó:

Ehhez próbáltam olyan elemeket találni, hogy az összeállított játékból ne lehessen kivenni azonnal az egyik elemet, hanem előbb néhányat — lehetőség szerint minél többet — el kelljen mozdítani (hisz ezt nevezzük magasabb fokozatnak).

A tangram a kirakós logikai játékok egyik legismertebb csoportja. Nagyon sokféle hasonló játék létezik a tojás alakú tangramtól a szív alakúig. Az V. Országos Ördöglakat Találkozóra az ötös szám jegyében Gáspár Merse Előd egy olyan tangram változatot készített, amelynek minden tagja ötszög. Az alkotó koncepciója az volt, hogy csak rácsötszögek szerepeljenek a készletben, azaz olyan ötszögek, amelyeknek a csúcsai egy négyzetrács csúcsaira esnek, továbbá az, hogy legfeljebb két különböző oldalhosszúság szerepeljen. Rácsegységekben mérve a használt oldalhosszak nem mások lettek, mint kettő és gyök öt. Ez utóbbi az egy és kettő hosszúságú szárakkal rendelkező derékszögű rácsháromszög átlójának hossza. Ezen két oldalhosszúság közti relatív különbség csupán 12% körüli, ami odafigyelést igényel a játék során, ezért segítséget jelenthet, ha az ötszögek éleit hosszuk alapján két színnel színezzük. A fenti feltételeknek összesen tíz különböző rácsötszög felel meg. Így összesen 5+5 elem szerepel a pentangramra keresztelt játékban, természetesen mindez az ötös szám jegyében. A kirakó érdekessége, hogy az elemek között szerepelnek konkáv alakzatok is, és a pentominó és más kirakós játékokhoz képest szakít a derékszögekkel. A pentangram további érdekessége, hogy a hagyományos tangramokhoz képest inverz módon jött létre, azaz nem egy meglévő alakzatot vagdosott részekre az alkotó, hanem adott tulajdonságoknak eleget tevő összes ötszög alakú elemet vette számba.

Mostanában sokszor gondolkodom a a különböző játékok nehézségén. Mitől függhet? Vannak-e határai? Érdemes-e olyan játékokat kitalálni, amelyek megoldására, elsőre úgy tűnhet, hogy esély sincs? Kísérletet sem teszek ezen kérdések megválaszolására, de a most bemutatandó játékok is komoly dilemma elé állítottak. Esélyem sem volt a megoldásukra, minden kísérletem rettentő távol állt a helyes megoldástól. Másrészt viszont látszólag nagyon egyszerű elemekből állnak, mindössze 4 L-ből. Az L-ek közül 2 pentominó és 2 tetrominó. Az egyik oldaluk:

Minden elemet a helyén hagyva, de átfordítva a másik oldalra:

Már sok kockakirakóval találkozhattunk a blogon. Bemutattuk a Szóma kockát, e játéktípus legismertebb tagját. Volt szó a több nehézségű Hannappel kockáról, a viszonylag egyszerű elemekből álló kockákról, a pentakockákból alkotható kockákról és más hasonló összerakók is szerepeltek már. Ezeknek közös jellemzője volt, hogy 3 egység oldalú kockákat kellett összeállítani olyan elemekből, amik 1 egységnyi kockák összeerősítésével keletkeznek.

A pentakockás bejegyzésben láthattuk, hogy 5 és 4 kockából álló, térbeli elemeket felhasználó összerakó közel 200-féle létezik. Igazából megbecsülni sem tudom, hogy hányféle összerakó játék létezhet, ha nem kötjük ki, hogy az elemek 4-5 kockából állhatnak csak. Több ezer? Több millió? Fogalmam sincs, de inkább az utóbbira gondolnék.

Nem  véletlen, hogy sok, híres játéktervező fantáziáját is megmozgatta e játéktípus. Nob Yoshigahara még csavart egyet a játékon, így született a csomós kocka.

Az élő legenda, Stewart Coffin "egyszerűen" megadott hat elemet:

Ezekből kell egy kockát összerakni.

A "kissé" szenzációhajhász cím talán indokolt, ha ha figyelembe vesszük az előzményeket. A Félkész őrület nevű játékról szóló bejegyzés elég népszerű volt. Jópáran elkészítették a színes kockákat és több kérdés is felmerült. Meg izgatott a probléma, hogy vajon csak a véletlen, hogy létezik ilyen kockakészlet? Egyáltalán van másik hasonló? Több vagy kevesebb kockából, színből is lehet hasonlót alkotni?

Belekezdtem egy nagyobb számítógépes vizsgálatba és bizony jutottam néhány érdekes eredményre. Ezekről szól  ez a bejegyzés.

Először nézzük a már bemutatott négy kockából és négy színből álló változatot! Adott tehát 4 kocka, az oldalaik 4 színnel vannak színezve. Minden kocka különböző. A feladat szerint egy tornyot kell készíteni belőlük úgy, hogy a torony minden oldalán csupa különböző színű oldal látszódjon:

A fotón csak 2 hosszú oldal látszik, azokon tényleg különbözőek a színek. (Elárulom, hogy ebben az elrendezésben a két nem látszó oldalon nem így van, nem akartam lelőni a megoldást.)

A nemzetközi ördöglakat találkozóról vagyis az IPP-ről már többször volt szó ezen a blogon. Bemutattam az előkészületeket, a főbb eseményeket és két onnan származó ajándékot is. Volt szó az eddigi legnagyobb (és lényegében felülmúlhatatlan) magyar sikerről, a SmartEgg-ről. Részletesen bemutatta az alkotó az egyik magyar csere- és versenyjátékot. A következőkben szintén egy IPP-s játékról lesz szó, ráadásul olyan típusról, ami viszonylag ritkán szerepel nálunk. Nem vagyok túl jó a labirintusokban, sem a készítésben, sem a megoldásban nem jeleskedem, de elismeréssel és csodálattal nézem e játéktípus mestereit.

Az IPP-n az "egyenruha" egy olyan póló volt, ami (természetesen) szintén felfogható volt játéknak. Azzal az apró szépséghibával, hogy pont a viselője nem tudott játszani vele, hisz a feladványok a hátulján szerepeltek:

Egy játék kategóriába sorolásánál fontos szempont, hogy két vagy három dimenziós. Általában a térbeli fejtörők a népszerűbbek, bár van néhány nagyon jól eltalált síkbeli összerakó is. Vannak azonban igazán meglepő ördöglakatok is, amik átmenetet képeznek a tér kiterjedései között. Ilyet alkotott Hiroshi Yamamoto többszörös díjnyertes játéktervező. Általában nagyon egyszerűnek tűnő fejtörőket tervez, csak amikor kipróbáljuk, akkor döbbenünk rá, hogy mennyire csal a látszat, a könnyűnek tűnő elemek mennyire komoly fejtörést kívánnak.

A magasságuk 4 és 7 egység között változik, a szélességük pedig 3 vagy 4 egység.

Egy jó játék sokakat inspirál továbbgondolásra. Nehezebb változatok vagy épp könnyebbek jelennek meg, kicsi vagy nagy átalakításokkal új, érdekes mutánsok születnek. A Hanoi torony is ilyen játék, sok játéktervező fantáziáját mozgatta meg.

Az egyik érdekes ötlet kétféle színű korongok használata:

Van az ördöglakatoknak, logikai játékoknak egy olyan csoportja, amiről eddig még nem volt szó a blogon. A rendszerezésnél már említettem, de ott konkrét példa nélkül. Most bemutatom egy jellemző képviselőjét. Ez a csoport nem más, mint a lehetetlen tárgyak osztálya. Kissé kilóg az ördöglakatok közül, hisz itt a kész "játékkal" már nem kell csinálni semmit, nem kell levenni, összerakni, szétszedni, bepakolni... Egyszerűen rá kell jönni, hogy hogyan is készült. Itt tehát maga az elkészítés módja a feladvány.

Lássuk az egyik leghíresebb változatot:

Amint a képen is látható, egy sértetlen, lyukas pénzérmén hatol át egy sértetlen nyílvessző.

Sokszor foglalkoztunk már a 6 elemű rabkeresztekkel. Ebben a bejegyzésben részletesen írtam a játék történetéről, arról a hatalmas kutatómunkáról, amit Bill Cutler végzett, hogy e játékcsalád minden csínját-bínját felderítse. Kiderítette, hogy több milliárd különböző kereszt létezik, ezek között vannak egészen könnyűek és rettentő nehezek is. Néhány rekorderről már volt szó itt és még fogunk is más csúcstartókat elemezni. Bill Cutler az összes lehetséges esetet vizsgálta, így sokáig azt hihettük, hogy már nem hozhat lényeges újdonságot a 6 elemű rabkeresztek világa.

Ebben a tanévben két japán egyetemista úgy határozott, hogy informatikai szakdolgozatukat a magasabb fokozatú rabkeresztek elemzéséből készítik. E témakör számos ma még tisztázatlan kérdést rejt, érdemes foglalkozni vele, ha nem is könnyen, de lehet elérni olyan eredményeket, amikre az egész játékvilág felkapja a fejét. Japánban egyébként is nagy kultusza van a míves játékoknak.

Izumo Asikaga és Ise Taisa természetesen Bill Cutler tanulmányait is olvasták, így ismerték az általa elért eredményeket. Tudták, hogy Cutler elemzése szerint a 6 elemű rabkeresztek közül a legmagasabb fokozatú 12-es, de ennek a keresztnek több, ennél kisebb fokozatú megoldása is létezik. (A fokozat fogalmáról már többször volt szó, röviden ismét: Egy rabkereszt fokozata az a szám, ahányszor el kell mozgatni néhány elemet, mire az elsőt ki lehet venni.) Az egy megoldással rendelkező 6 elemű rabkeresztek közül a legmagasabb fokozat a 10-es. (Erről még nem volt szó a blogon, de ami késik, nem múlik.)

Asikaga és Taisa észrevett valamit, ami először nem is tűnt túl érdekesnek, de ahogy egyre alaposabban belemélyedtek a témába, egyre nagyobb jelentőségűnek látszott. Feltűnt nekik, hogy Cutler nem foglalkozott az elemek hosszával. Első (és második meg harmadik) átgondolásra ennek nincs is jelentősége, hisz miért bonyolítana egy megoldást, ha a szerkezet ugyanaz, csak hosszabb elemekből áll. Szerencsére a két japán srác negyedszer is átgondolta kérdést és legnagyobb megdöbbenésükre találtak egy keresztet, ami ellentmondani látszott Cutler eredményeinek:

Mondtam már, hogy szeretem a kevés elemből álló, mégis nehéz játékokat? Mondtam hát, többször is, pl. itt vagy itt.

Most ismét ebbe a családba passzoló rabkeresztek következnek. Sőt, rögtön egy új családba is betekintést nyerünk, mégpedig a "rabkereszt sorozatok"-ba.

Mozart Varázsfuvolája ihlette Gregory Benedetti francia játéktervezőt e játékcsalád megalkotására. Vagy legalább a játékok elnevezését merítette az operából. Az összerakott játék tényleg hasonlít egy pánsípra:

Az elősző Hoppersről szóló cikkbe egy súlyos hiba csúszott. Rosszul készítettem el a játék tábláját, így néhány vonal lemaradt róla. Sajnos, ezt nem én vettem észre, hanem már a bejegyzés megjelenése után egy figyelmes olvasó. Még egyszer köszönöm sebcsabának!

Íme egymás mellett a jó és a hibás Hoppers tábla:

A bal oldali a helyes, a jobb oldali a hibás. Ezután azt Félhoppersnek fogom hívni.